Rotation autour d’un axe fixe

Après avoir défini les grandeurs et les théorèmes de la mécanique du solide, il nous reste à appliquer ces théories à des cas pratiques. Le premier exemple que nous avons traité était celui des particules chargées où l’on se ramenait à la dynamique du point.

Dans le cas de la dynamique du solide, trois cas sont envisageables pour le mouvement du solide :

- un mouvement de translation,

- un mouvement de rotation,

- la combinaison des deux précédents.

Le traitement du mouvement de translation est similaire aux traitements de dynamique du point.

Nous allons donc dans ce chapitre traiter les mouvements de rotation en l’absence de mouvement de translation.

Pour éviter de rentrer dans des traitements mathématiques matriciels qui apportent peu d’éléments supplémentaires à la compréhension physique des mouvements de rotation, on se restreindra à l’étude de solides ayant une symétrie sphérique ou cylindrique.

2.6.1 Moment d’inertie

Lors de mouvement de rotation, la répartition des masses du solide par rapport à l’axe de rotation est une caractéristique essentielle.

Il est nécessaire de bâtir une grandeur intrinsèque au solide qui prenne en compte cette répartition de masse.

La première idée pourrait être de définir d’une part une grandeur :

masse χ distance à l’axe .

Mais la distance à l’axe apparaîtrait de nouveau dans l’expression de la vitesse de chaque point selon la relation, lors du calcul du moment cinétique.

On définit donc la grandeur intrinsèque:

masse χ distance à l’axe χ distance à l’axe

soit :

2.6.1.1 Moment d’inertie par rapport à un axe

En prenant H_i le projeté orthogonal sur l’axe de rotation Δ de chaque point A_i affecté d’une masse m_i.

Si la distribution de masse est discrète on le calcule par.

Si la distribution de masse est continue on le calcule par avec ρ_m la masse volumique notée ainsi pour ne pas la confondre avec le rayon polaire ρ.

Expressions par rapport aux axes du repère cartésien

En coordonnées cartésiennes :

Si Δ est l’axe Ox :

Si Δ est l’axe Oy :

Si Δ est l’axe Oz :

En coordonnées cylindriques :

Si Δ est l’axe Oz : avec soit :

2.6.1.2 Moment d’inertie par rapport à un point

Pour des raisons de facilité de calcul, il peut être intéressant de définir le moment d’inertie par rapport à un point

En effet dans le cas d’une symétrie sphérique les axes Ox, Oy, et Oz sont équivalents et on a :

et donc :

avec

et donc pour les solides à symétrie sphérique:

2.6.1.3 Base principale d’inertie

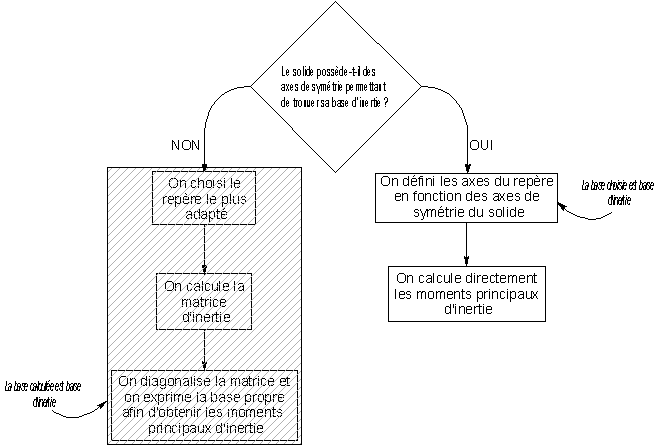
Lors du mouvement de rotation d’un solide, l’axe de rotation ne correspond pas forcément aux axes de symétrie du solide.

Si le solide possède des axes de symétrie le choix des axes du repère s’en déduit afin de faciliter les calculs.

En effet :

Tout axe de symétrie matérielle est axe principal d’inertie

Tout axe perpendiculaire à un plan de symétrie matérielle est axe principal d’inertie

On pourra donc très souvent être confronté à définir des moments d’inertie par rapport à un axe de rotation qui ne correspond pas aux axes de symétrie du solide.

Aussi toujours afin de faciliter les calculs, va-t-on procéder ainsi :

Dans ce cours on va se limiter aux solides à symétrie cylindrique et sphérique et donc la base cartésienne sera une base principale d’inertie et on aura :

- pour la symétrie sphérique

- pour la symétrie cylindrique

Donc on calculera d’abord ces moments d’inertie puis on en déduira le moment d’inertie par rapport à notre axe Δ quelconque par la relation simple :

où l’axe Δ est de vecteur directeur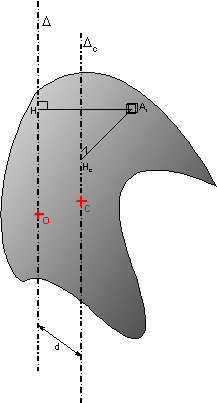

2.6.1.4 Théorème d’Huyghens-Schteiner

Ce théorème permet de lier le moment d’inertie par rapport à un axe quelconque avec le moment d’inertie d’un axe parallèle passant par le centre d’inertie du solide.

En effet on a :

avec et donc

2.6.1.5 Exemples de calculs de moments d’inertie

Moment d’inertie d’un disque plein

La symétrie est cylindrique on prend donc :

Le volume d’un disque de rayon R et d’épaisseur h est donc :

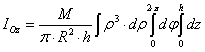
Moment d’inertie d’un cône plein régulier

Le cône est homogène de rayon R au sommet et de hauteur h

La masse du cône est (cf 1.4.5.3.1) donc

Calculons le moment d’inertie par rapport à l’axe Oz : I_z

On va utiliser le résultat précédent en considérant le cône comme un empilement de disques de rayon r :

avec

et (cf 1.4.4.3.3)

On obtient :

Moment d’inertie d’une sphère creuse

Comme pour le calcul du centre d’inertie on se ramène à des calculs sur les éléments de surface.

La symétrie sphérique permet de calculer le moment d’inertie par rapport au point O et d’en déduire le moment d’inertie par rapport à l’axe selon

L’élément de surface est alors

Comme on l’a vu en 1.4.4.2.2 la surface d’une sphère vaut et donc

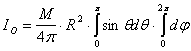
Moment d’inertie d’une sphère pleine

La symétrie sphérique permet de calculer le moment d’inertie par rapport au point O et d’en déduire le moment d’inertie par rapport à l’axe selon

L’élément de volume est :

Comme on l’a vu en 1.4.4.3.2 le volume d’une sphère vaut et donc

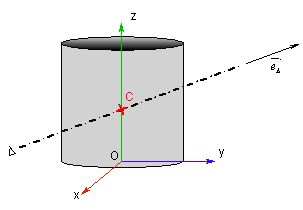
2.6.2 Cas d’un solide à symétrie cylindrique ou sphérique

Dans le cas du solide à symétrie cylindrique ou sphérique les axes du repère correspondent avec les axes principaux d’inertie.

Les relations fondamentales ci-dessous conservent toute leur généralité, mais pour les appliquer dans le cas général telles vont être présentées ici, il sera nécessaire de recourir à des calculs matriciels de produits d’inertie pour se placer dans la base principale d’inertie.

2.6.2.1 Moment cinétique - Moment d’inertie

Soit la rotation de ce cylindre autour de l’axe Oz nommé Δ

L’expression du moment cinétique :

Peut s’écrire sachant que :

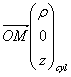
Et que pour tout point M situé à une distance R de l’axe de rotation on a :

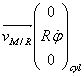
Le produit vectoriel donne :

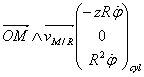
d’où l’expression du moment cinétique :

où la projection sur l’axe de rotation Oz du moment cinétique s’écrit :

2.6.2.2 Théorème du moment cinétique par rapport à l’axe de rotation

La projection du moment cinétique et du moment des forces par rapport à l’axe de rotation permet d’écrire :

2.6.2.3 Expression de l’énergie cinétique d’un solide en rotation autour d’un axe fixe

On sait que :

Dans le cas d’un solide en rotation ayant un point fixe l’expression de l’énergie se simplifie.

On a vu en 2.2.2 que l’expression de la vitesse est dans ce cas :

Ce qui permet d’écrire :

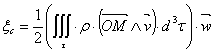
Dans le cas de la rotation autour de l’axe de direction fixe passant par le point O on a :

ce qui permet d’écrire :

2.6.2.2 Analogie avec le mouvement de translation

On peut faire apparaître l’analogie grâce au tableau suivant :

Grandeur	Translation selon l’axe Ox	Rotation autour de l’axe Δ
Energie cinétique
Théorème fondamental
Torseur cinétique

Ceci nous permet de mieux nous rendre compte de l’importance de moments d’inertie dans la compréhension physique des mouvements de rotation.

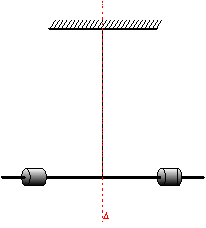2.6.3 Exemples

2.6.3.1 Mouvements pendulaires

Le pendule de torsion

L’application du théorème du moment cinétique au pendule soumis à un couple de torsion de moment de rappel où C est la constante de torsion donne l’équation différentielle:

traduisant un mouvement oscillatoire de pulsation

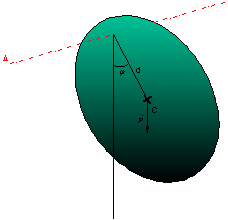
Le pendule pesant

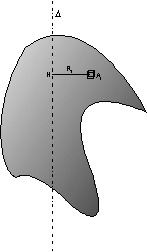
L’application du théorème du moment cinétique à ce disque de masse m tournant autour d’un axe Δ distant d’une distance d du centre de masse C donne avec le moment du poids

l’équation différentielle :

qui dans le cadre des faibles oscillations peut s’approximer par :

traduisant un mouvement oscillatoire de pulsation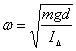

avec

Le pendule simple

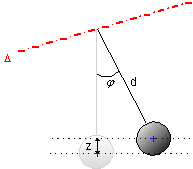Pour le pendule simple on va utiliser le théorème de l’énergie mécanique.

Le pendule constitué d’une sphère de rayon r et de masse m suspendue à une tige de masse négligeable devant la sphère.

On a :

L’énergie potentielle de pesanteur est prise égale à 0 pour z=0, on a donc avec l’expression :

L’énergie cinétique vaut :

Le théorème de l’énergie mécanique donne : soit et donc l’équation différentielle :

C’est une équation avec 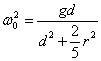du type : qui en dérivant donne une équation du type : comme le cas précédent du pendule pesant.

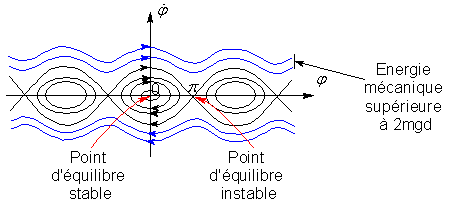
Etudions un peu plus en détail le mouvement du pendule à l’aide du portrait de phase qui est la représentation en abscisse du degré de liberté (ici ) et de sa dérivée en ordonnée (ici ). D’après l’équation différentielle ci-dessus on a