Rappels de mathématiques
http://convergence.chez.tiscali.fr/phys/sup/meca
1. Prérequis de mathématiques et de physique
1.4.1 Coordonnées cartésiennes
1.4.2 Coordonnées cylindriques
1.4.4 Application aux calculs de surfaces et de volumes
1.4.5 Application aux calculs de centre d’inertie
1.6.4 Relations entre opérateurs
1. Prérequis de mathématiques et de physique
1.1. Les intégrales
1.1.1 Définitions
Primitive
Soit f une fonction réelle ou complexe définie dans un intervalle I. On appelle primitive de f toute fonction réelle ou complexe définie dans I telle que F’=f
Intégrale
Soient (x0, x1, x2,…., xn) une subdivision de [a,b] telle que la fonction f ait une valeur constante ci dans chaque intervalle ]xi,xi+1[, on appelle intégrale de f le nombre réel :
c0(x1-x0)+c1(x2-x1)+…..+cn(xn-xn-1)
Ce nombre se note :
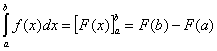
1.1.2 Propriétés
Intégrales équivalentes : 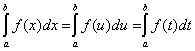
Multiplication par une constante :
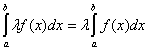
Intégrale d’une somme : 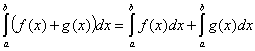
Valeur absolue d’une intégrale : 
Intervalles contigus : 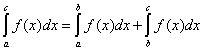
Opposée de l’intégrale : 
Valeur moyenne : 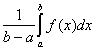
1.1.3 Méthodes d’intégration
En notant ![]() et
et
![]() les dérivées simples et doubles par
rapport au temps t.
les dérivées simples et doubles par
rapport au temps t.
Intégration par parties : ![]()
Changement de variable ![]() :
:  avec
avec
![]() et
et ![]()
1.2 Les différentielles
Forme différentielle :
![]()
Différentielle exacte :
Si A1, A2 et A3 sont les dérivées d’une même fonction A telles que :
![]() ,
, ![]() et
et ![]() alors
c’est une différentielle exacte :
alors
c’est une différentielle exacte : ![]()
La distinction entre différentielle et forme différentielle est importante car on ne peut calculer la valeur de W entre deux points x1 et x2 qu’avec une différentielle :

Dans le cas d’une forme différentielle, ce calcul n’est pas directement possible, W dépend du chemin suivi entre les deux points x1 et x2.
1.3 Equations différentielles
1.3.1 Solutions types
![]() de solution
de solution ![]()
![]() de solution
de solution ![]()
![]() de solutions
de solutions 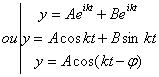
![]() en posant
en posant ![]() de solutions
de solutions 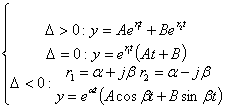
1.3.2 Méthode de résolution
Dans le cas d’une équation différentielle inhomogène (avec un second membre) on procède en deux temps :
● On prend une solution du type du second membre avec des constantes à déterminer et on remplace dans l’équation différentielle inhomogène pour obtenir la valeur des constantes.
● On cherche la solution de l’équation homogène.
Puis on additionne les deux solutions.
Exemple : Soit à
résoudre ![]() où C est une constante
où C est une constante
● ![]() soit en
remplaçant
soit en
remplaçant ![]() et donc
et donc ![]()
● ![]() de
solution
de
solution ![]()
d’où la solution générale : ![]()
1.4 Coordonnées
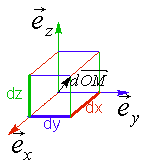
1.4.1 Coordonnées cartésiennes
Coordonnées :
x : abscisse
y : ordonnée
z : côte
Représentation :
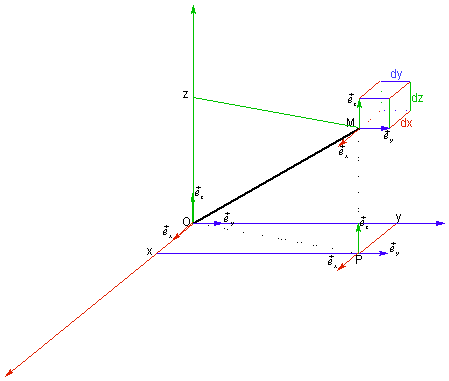
Vecteur position :
![]()
![]()
Déplacement élémentaire :
![]()
Volume élémentaire :
![]()
1.4.2 Coordonnées cylindriques
 Coordonnées :
Coordonnées :
r : rayon polaire
j : angle polaire
z : côte
Représentation :
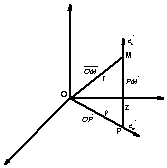
Vecteur position :
![]()
![]()
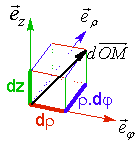
Déplacement élémentaire :
![]()
Volume élémentaire :
![]()
Relation avec les coordonnées cartésiennes :
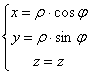
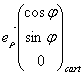
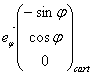
![]()
![]()
![]()
![]()
![]()
![]()
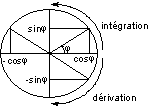
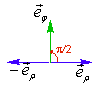
On remarquera que la dérivation par rapport à ![]() correspond à une rotation de
correspond à une rotation de ![]() :
:
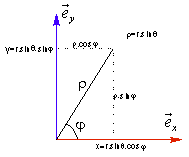
1.4.3 Coordonnées sphériques
Coordonnées :
r : rayon
vecteur ![]()
q :
colatitude
![]()
j :
azimuth
![]()
Représentation :
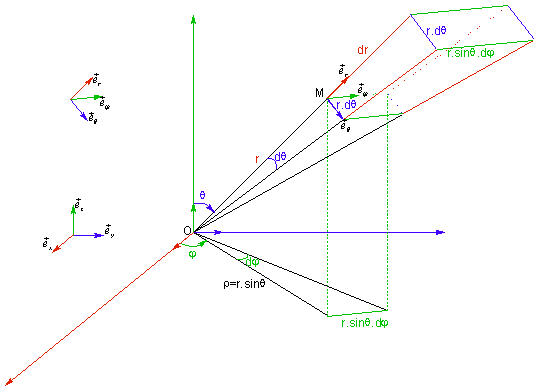
 Vecteur position :
Vecteur position :
![]()
Déplacement élémentaire :
![]()
Volume élémentaire :
![]()
Relation avec les coordonnées cartésiennes :
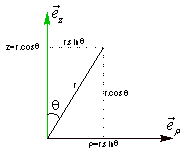
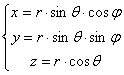
1.4.4 Application aux calculs de surfaces et de volumes
1.4.4.1 Formulaire
4.4.1.1 Coefficients
|
|
d1 |
d2 |
d3 |
|
Coordonnées cartésiennes |
dx |
dy |
dz |
|
Coordonnées cylindriques |
dr |
dj |
dz |
|
Coordonnées sphériques |
dr |
dq |
dj |
|
|
|
|
|
|
Coordonnées cartésiennes |
|
|
|
|
Coordonnées cylindriques |
|
|
|
|
Coordonnées sphériques |
|
|
|
|
|
c1 |
c2 |
c3 |
|
Coordonnées cartésiennes |
1 |
1 |
1 |
|
Coordonnées cylindriques |
1 |
r |
1 |
|
Coordonnées sphériques |
1 |
r |
r.sinq |
Déplacement
élémentaire ![]()
4.4.1.2 Calcul de surfaces
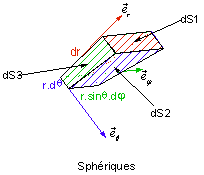

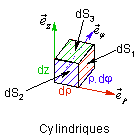
|
|
dS1 |
dS2 |
dS3 |
|
Cartésienne |
dy.dz |
dx.dz |
dx.dy |
|
Cylindrique |
dz.rdj |
dr.dz |
dr.rdj |
|
Sphérique |
r.dq.r.sinq.dj |
dr.r.sinq.dj |
r.dq.dr |
|
général |
c2.d2.c3.d3 |
c1.d1.c3.d3 |
c1.d1.c2.d2 |
4.4.1.3 Calcul de volumes
Comme pour le calcul de surface il est nécessaire pour ce calcul d’exprimer l’élément de volume qui permet de trouver les bornes d’intégration les plus simples.
![]()
1.4.4.2 Exemples de calculs de surfaces
4.4.2.1 Surface d’un cercle
Les repères cylindrique ou sphérique peuvent être utilisés dans ce cas.
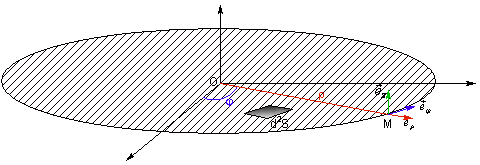
Si l’on choisi la notation cylindrique on a une surface dans
le plan ![]() ,
,
et donc un élément de surface ![]()
avec r variant de 0 à R et j de 0 à 2p :
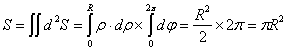
1.4.4.2.2 Surface d’une sphère
Le repère sphérique doit être utilisé dans ce cas.
Le rayon de la sphère est constant et égal à R.
Chaque élément de surface est dans le plan défini par ![]() et vaut :
et vaut : ![]()
Il est important de noter que la surface complète de la sphère correspond à:
q variant de 0 à p
et j variant de 0 à 2p
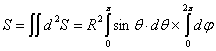
![]()

1.4.4.3 Exemples de calculs de volumes
1.4.4.3.1 Volume d’un cylindre
Le repère cylindrique s’impose naturellement.
Pour un cylindre de rayon R et de hauteur h on a un
élément de volume ![]()
Et un volume
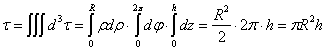
1.4.4.3.2 Volume d’une sphère
Le repère sphérique s’impose naturellement.
Le rayon de la sphère est constant et égal à R.
L’élément de volume est ![]()
Et un volume

1.4.4.3.3 Volume d’un cône
Le repère cylindrique s’impose.
Pour un cône régulier de rayon R au sommet et de hauteur h.
On exprime l’élément de volume par ![]() comme étant une superposition
de disques de hauteur infinitésimale dz.
comme étant une superposition
de disques de hauteur infinitésimale dz.
En remarquant que r est fonction de z, on l’exprime
grâce à la relation de Thales ![]() et
ainsi
et
ainsi ![]()
Et un volume
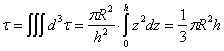

1.4.5 Application aux calculs de centre d’inertie
1.4.5.1 Définition du centre d’inertie
Le centre d’inertie C (ou centre de masse) est le barycentre des points du système pondéré par leur masse.
Il est nécessaire de le connaître pour localiser le point d’application du poids d’un corps et pour les mouvements de translation.
Si la distribution de masse est discrète on le
calcule par ![]() avec M la masse
totale du système.
avec M la masse
totale du système.
Si la distribution de masse est continue on le
calcule par ![]() avec ρ la masse
volumique.
avec ρ la masse
volumique.
On peut aussi écrire ![]() et
donc
et
donc 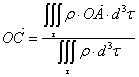
1.4.5.2 Propriétés du centre d’inertie
Associativité : Deux systèmes de centres et de masses respectifs C1,C2,m1,m2 ont pour centre de masse :
![]()
Symétrie matérielle : Si un système possède un élément de symétrie matérielle qui vérifie pour tout point A :
![]()
Alors l’élément de symétrie contient le centre de masse.
1.4.5.3 Calculs de centres d’inertie
1.4.5.3.1 Centre d’inertie d’un cône plein régulier
Le cône est homogène de rayon R au sommet et de hauteur h
Le volume du cône est ![]() (cf
1.4.4.3.3) et donc sa masse
(cf
1.4.4.3.3) et donc sa masse ![]()
La symétrie matérielle indique que le centre d’inertie
appartient à l’axe Oz. Il suffit donc de calculer la coordonnée zc
du centre d’inertie
selon :
![]() avec
avec ![]() (cf 1.4.4.3.3)
(cf 1.4.4.3.3)
On
obtient :
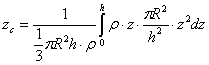
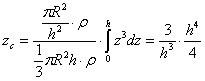
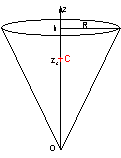
![]()
1.4.5.3.2 Centre d’inertie d’une demi sphère pleine
Le volume d’un demi sphère est ![]() (cf
1.4.4.3.2) et donc sa masse
(cf
1.4.4.3.2) et donc sa masse ![]()
La symétrie matérielle indique que le centre
d’inertie appartient à l’axe Oz. Il suffit donc de calculer la coordonnée zc
du centre d’inertie
selon :
![]()
avec ![]() (cf 1.4.4.3.2) et
(cf 1.4.4.3.2) et ![]()
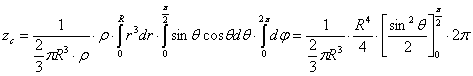
![]()
1.4.5.3.3 Centre d’inertie d’une demi sphère creuse
La symétrie matérielle indique que le centre d’inertie appartient à l’axe Oz. Il suffit donc de calculer la coordonnée zc
Pour la demi sphère creuse le rayon est constant et égal à R, on peut faire le calcul sur des éléments de surface, et définir une densité massique de surface ρS :
![]() avec
avec ![]()
L’élément de surface est alors ![]() et on a
et on a ![]() :
:
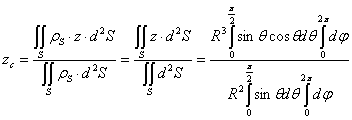
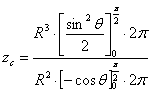
![]()
1.4.5.3.4 Centre d’inertie d’un disque percé
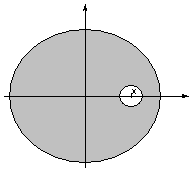
Un disque de rayon R1 est percé à l’abscisse x d’un trou circulaire de rayon R2
L’axe Ox est axe de symétrie on calcule donc uniquement l’abscisse du centre de masse.
La masse du disque non percé vaut :![]()
La masse évidée vaut :![]()
La masse du disque percé vaut :![]()
L’abscisse se calcule en utilisant la propriété d’associativité rappelée en 1.4.5.2
On notera que l’abscisse du cercle non percé est nulle et que la masse évidée est considérée comme négative dans le calcul.
![]()
![]()
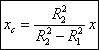
1.4.5.3.5 Centre d’inertie d’un solide simple

Un solide est composé de deux parallélépipèdes rectangles de cotés a, 3a et e pour le premier et a, 2a et e pour le second.
Les coordonnées respectives des deux centres d’inertie des deux solides sont :
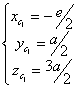 et
et 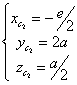
Les masses respectives :
![]() et
et ![]() et la masse totale
et la masse totale ![]()
d’où les coordonnées du centre d’inertie :
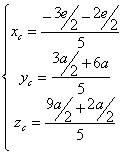
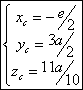
1.5 Les Vecteurs
Vecteur libre : Vecteur défini uniquement par sa direction son sens et sa valeur, son point d’application pouvant être quelconque dans l’espace.
Vecteur glissant : Vecteur défini uniquement par sa droite d’action son sens et sa valeur, son point d’application pouvant être quelconque sur la droite d’action.
Vecteur lié : Vecteur défini par sa droite d’action son sens, sa valeur et son point d’application.
Moment en un point d’un vecteur lié : Le
moment ![]() en O d’un vecteur
en O d’un vecteur ![]() de point d’application A
vaut :
de point d’application A
vaut :
![]()
Torseur : C’est l’ensemble constitué du
moment et de son vecteur![]() .
.
Moment par rapport à un axe d’un vecteur lié :
Le moment ![]() par rapport à l’axe
Δ passant par O de vecteur unitaire
par rapport à l’axe
Δ passant par O de vecteur unitaire ![]() d’un
vecteur
d’un
vecteur ![]() de point
d’application A vaut :
de point
d’application A vaut :
![]()
Somme géométrique de vecteurs : La somme géométrique de vecteurs libres, glissant ou lié est un vecteur libre.
Résultante de vecteurs : C’est un cas particulier de somme géométrique de vecteurs glissant ou lié. Elle n’existe que si les vecteurs sont concourants au même point ou parallèles et de même sens. Si les vecteurs sont liés, la résultante est un vecteur lié, ainsi par exemple la résultante des vecteurs poids élémentaires est une vecteur poids dont le point d’application est le centre de gravité du solide considéré.
Produit scalaire : C’est le nombre réel ![]() qui est une grandeur
intrinsèque (indépendante de la base de calcul). Soient les vecteurs
qui est une grandeur
intrinsèque (indépendante de la base de calcul). Soient les vecteurs ![]() et
et ![]() on
a
on
a ![]()
Produit vectoriel : C’est un vecteur
libre ![]() dont le sens est tel qu’il
forme un trièdre
dont le sens est tel qu’il
forme un trièdre ![]() positif,
dont la direction est perpendiculaire au plan formé par les vecteurs
positif,
dont la direction est perpendiculaire au plan formé par les vecteurs![]() , et de norme
, et de norme![]() .
.
Le sens du vecteur dépend de l’orientation de l’espace choisi et défini par la règle de la main droite.
On a aussi avec ![]() et
et
![]() :
: 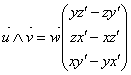
1.6 Les opérateurs
Ils permettent d’exprimer localement des relations intégrales.
1.6.1 Le gradient
Cet opérateur vectoriel agit sur un scalaire. Il est le vecteur normal à la surface de niveau (surface où V est constant) dirigé dans le sens des V croissants.
![]()
En utilisant les notations vues en A.4.4.1 :
![]()
Soit par exemple en coordonnées sphériques :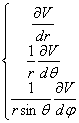
1.6.2 La divergence
Cet opérateur scalaire agit sur un vecteur.
Cette valeur correspond au flux ![]() du
vecteur
du
vecteur ![]() sortant d’une unité de
volume à travers une surface fermée.
sortant d’une unité de
volume à travers une surface fermée.
![]()
En utilisant les notations vues en A.4.4.1 :
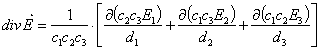
Soit par exemple en coordonnées cartésiennes : ![]()
1.6.3 Le rotationnel
Cet opérateur vectoriel agit sur un vecteur.
Ce vecteur est parallèle à la normale du plan pour lequel la circulation
élémentaire![]() est maximale.
est maximale.
![]()
En utilisant les notations vues en A.4.4.1 :
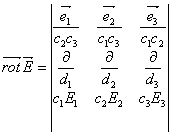 où
où ![]() est la notation d’un
déterminant.
est la notation d’un
déterminant.
Soit par exemple en coordonnées cartésiennes : 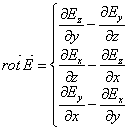
1.6.4 Relations entre opérateurs
![]()
![]()
1.6.5 Relations intégrales
Soient τ un volume limité par une surface S et une surface S limitée par une courbe fermée C.
Formule de Stokes : Circulation de E sur
la courbe fermée C ![]()
Formule d’Ostrogradsky : Flux de E
à travers une surface fermée S ![]()
Formule du rotationnel : ![]()
Formule du gradient : ![]()
Formule de Kelvin : ![]()