TD statique

 

Exercice 1 : La potence

Soit une potence constituée :

              - d’une barre métallique homogène de longueur AB=l₁=3,5m et de masse m=20kg

              - d’un câble horizontal de longueur BC=l₂=2,0m et de poids négligeable devant la tension

On suspend en B un câble de 1kg auquel est attaché une charge de 89kg.

              a) Faire un bilan des forces s’appliquant sur la barre. On nommera b l’angle que fait la réaction avec la verticale.

              b) Rappeler les conditions d’équilibre puis les exprimer en fonction des données du problème.

              c) En déduire la valeur de la tension du câble et de la réaction en A.

On prendra g=10 N/kg

Exercice 2 : La console mobile

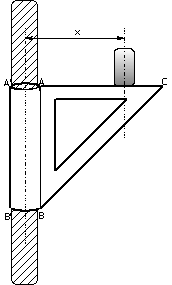Soit une console constituée d’un triangle rectangle isocèle ABC et tel que AB=AC=l.

Son poids est négligeable devant la charge portée sur AC.

Elle est installée sur un tuyau de diamètre 2r.

Soit k le coefficient de frottement de glissement entre la console et le tuyau.

Calculer la distance minimale x à l’axe du tuyau pour laquelle la charge P peut être supportée sans qu’il y ait glissement de la console.

Exercice 3 : L’échelle

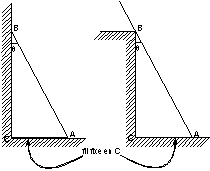
1) Soit une échelle de poids P en contact avec une paroi lisse et un sol lisse.

              a) Montrer que si les contacts se font sans frottement, il est impossible d’appuyer l’échelle obliquement contre un mur vertical.

              b) Dans les exemples ci-contre exprimer la réaction en A et B ainsi que la tension T du fil en fonction de P, l=AB et q.

2) On considère désormais dans la suite de l’exercice un sol rugueux, et l’échelle n’est plus maintenue par un fil.

       a) Calculer l’angle de frottement j pour maintenir juste l’échelle en équilibre. En déduire les réactions en A et B et le coefficient de frottement statique (l=5m, P₁=250N, q_max=30°)

       b) Exprimer la longueur l₁ en fonction de l’inclinaison q de l’échelle à laquelle un homme de poids P₂ peut monter. Faire l’application numérique avec un enfant de 30kg et un homme de 100kg pour un angle de 20°.

       c) Inversement exprimer la condition pour qu’un homme de poids P₂ puisse monter en haut de l’échelle. Faire l’application avec un homme de 70kg.

Version Word du TD : TD3.doc (286ko)