![]()
Etude d’un satellite géostationnaire
Rappels de cours
Puissance :
![]()
![]()
Travail :
![]() et
et ![]()
Energie cinétique :
![]()
Moment d’inertie par rapport à un axe si la distribution de
masse est discrète ou continue :
![]() ou
ou ![]()
En coordonnées cartésiennes :
![]()
![]()
![]()
Théorème d’Huyghens-Schteiner :
![]()
Moment cinétique par rapport à un axe :
![]()
Energie cinétique d'un solide en rotation:
![]()
Partie 1 Etude d’un panneau solaire
On souhaite réaliser l’asservissement de position d’un ensemble de panneau solaire dont la disposition est la suivante :
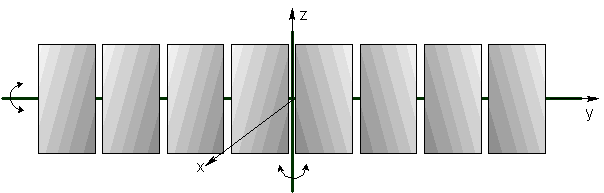
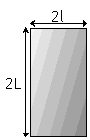
L’espacement entre chaque panneau solaire est de e=2cm. Chaque panneau a pour dimension 2l=50cm et 2L=1m et une masse m.
1° Calculer les moments d’inertie par rapport aux axes horizontaux et verticaux d’un panneau solaire.
2° En utilisant le théorème d’Huygens-Schteiner en déduire le moment d’inertie de l’ensemble selon l’axe Oy et l’axe Oz.
3° La vitesse de rotation du panneau vaut
![]() avec
avec ![]() et
et ![]() .
.
Exprimer puis calculer les moment cinétiques selon les axes Oy et Oz de l’ensemble des panneaux.
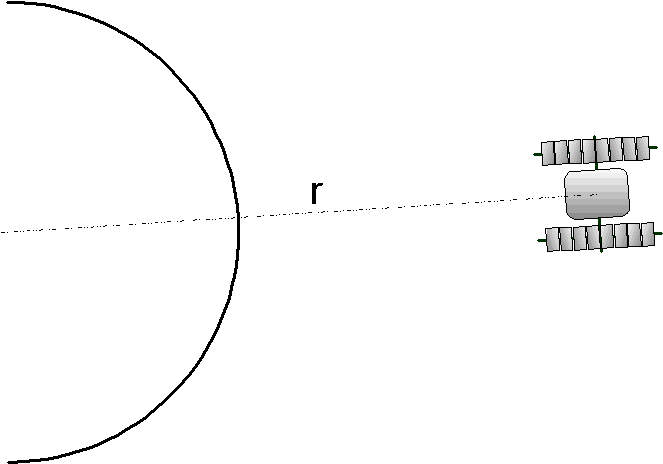
4° Calculer le couple moteur nécessaire à la mise en rotation de l’ensemble
en 24 h. Les frottements sont négligés.
Partie 2 Etude du satellite
Le satellite de masse M=3t est assimilable à une sphère pleine de 12m de diamètre.
1° Exprimer puis calculer le moment d’inertie de la sphère pleine.
2° Calculer l’énergie cinétique de ce satellite géostationnaire d’altitude r=40 000 km qui tourne sur lui-même en une minute.
Partie 3 Etude d’un pied de robot
Le pied d’un robot est constitué d’une demi-boule articulée.
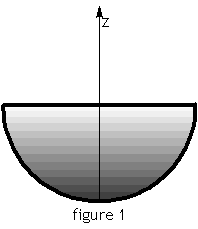
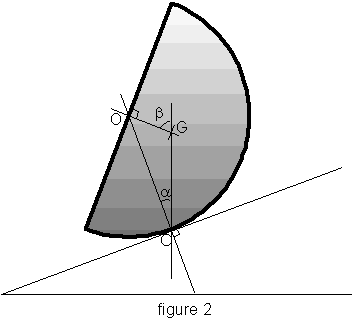
1° Déterminer la position du centre d’inertie de la demi-boule de rayon r
2° Déduire très simplement de la partie 2, le moment d’inertie d’une demi-boule selon l’axe Oz
La demi boule est en équilibre sur le plan incliné.
3° Faire un bilan des forces.
4° Exprimer les conditions d’équilibre.
5° En déduire la relation liant a et b.
6° En déduire la pente maximale admissible.