Rappels de cours
le travail :
l’énergie potentielle : 
l’énergie cinétique 
l'énergie mécanique
le théorème de l'énergie cinétique 
le théorème de l'énergie mécanique 
Exercice 1 : Saut à l’élastique
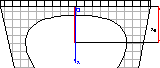
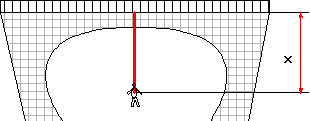
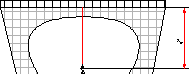
a) Faites un bilan des forces à l’équilibre
de cette personne de masse m=70kg suspendue à un élastique de raideur :
, longueur à vide :
8m et 
b) Calculez le travail des forces entre le haut du pont et une position quelconque xA (vous ferez apparaître les deux phases du mouvement).
c) Rappelez le théorème de l’énergie cinétique et exprimer la vitesse vA d’un point quelconque.
d) En déduire la longueur maximale atteinte.
e) Après avoir indiqué à quel moment de la trajectoire la vitesse est maximale vous la calculerez.
f) Après avoir indiqué à quel moment de la trajectoire la force de rappel est maximale vous la calculerez.
Exercice 2 : Mouvement d’une particule en interaction newtonienne ou coulombienne
Partie 1
a) Rappelez l’expression de la force de gravitation et de la force de Coulomb d’une particule de masse m et de charge q uniquement en interaction avec un système de masse M et de charge Q. Vous considérerez ce système comme origine du repère.
On notera désormais
sans distinction ces forces sous la forme 
b) Exprimer le moment de cette force par rapport à O.
Partie 2 éléments cinétiques
a) En appliquant le théorème du moment cinétique, en déduire la propriété du moment cinétique d’une particule soumis à une interaction Coulombienne ou Newtonienne.
b) Rappelez l’expression générale du moment cinétique de cette particule. Que pouvez-vous en déduire sur la nature du mouvement d’une particule soumis à une interaction Coulombienne ou Newtonienne.
c) En déduire en coordonnées cylindriques, les vecteurs position et vitesse.
d) En déduire les éléments cinétiques (Energie, quantité de mouvement et moment).
Partie 3 Travail et énergie potentielle
a) Exprimer le travail élémentaire
et montrer
que l’on peut définir une énergie potentielle.
b) Exprimer l’énergie mécanique.
Partie 4 Equation du mouvement
Pour rechercher
l’équation du mouvement on pose : 
et donc
a) Montrer que
l’on peut écrire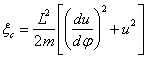 
b) En déduire l’expression de l’énergie mécanique
c) Calculer 
d) En appliquant le théorème de l’énergie mécanique et en utilisant le résultat précédent en déduire l’équation différentielle du mouvement (en u)
e) À l’aide de
votre cours de math, donner l’expression de u et en déduire l’expression de
.
Exercice 3 : Mouvement d’une particule dans une gouttière
Une particule de masse m est lâchée en A sans vitesse initiale et l’on cherche à savoir quelle doit être la hauteur h pour que la particule atteigne le point S sommet de la gouttière.
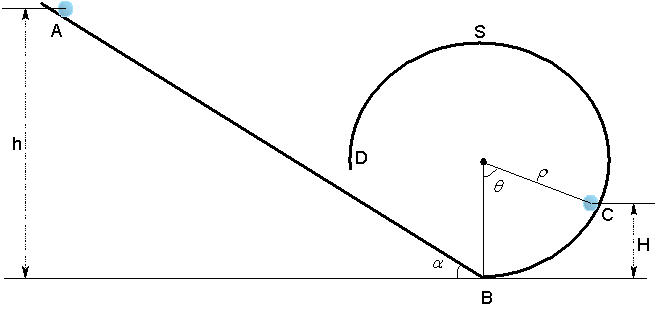
1° Indiquer sur le schéma ci-dessus les forces s’exerçant sur la particule aux deux points indiqués A et C.
2° Traitement scalaire :
a) Exprimer le travail des forces lors d’un déplacement élémentaire.
b) Exprimer l’énergie potentielle du poids.
c) Appliquer le théorème de l’énergie mécanique pour calculer la vitesse au point B.
d) Exprimer H en fonction de et 
.
e) Appliquer le théorème de l’énergie
mécanique pour calculer la vitesse au point C en fonction de H et de 
3° Traitement vectoriel :
a) Indiquer dans le repère intrinsèque à la partie BD, les coordonnées des vecteurs forces, vitesse et accélération.
b) En appliquant le théorème fondamental
de la dynamique, en déduire la valeur de la réaction R en fonction des données
suivantes : m,, , 
et g.
4°Indiquer la condition sur h pour que la bille atteigne le sommet S.