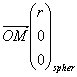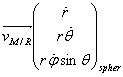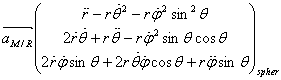INTERROGATION DE PHYSIQUE
Correction
I) QUESTIONS DE COURS 8 points
1° Démontrer en justifiant chaque étape de calcul l’expression du vecteur vitesse en coordonnées cylindriques.
On a vu que : 
donc on peut simplifier
et
car 
est un vecteur fixe
soit 
2° Démontrer en justifiant chaque étape de calcul l’expression du vecteur accélération en coordonnées cylindriques.
On a: donc et 
donc 
et
soit 
3° Rappeler sans démonstration l’expression du vecteur vitesse et du vecteur accélération en coordonnées intrinsèques.
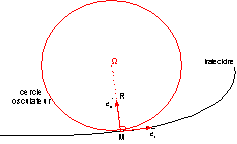
4° Donner les conditions d’équilibre, de translation, de rotation d’un solide.
Equilibre 
et 
Rotation 
Translation 
II) CINEMATIQUE 6 points
Un mobile considéré comme ponctuel est attaché à l’extrémité d’une barre de longueur L, mobile autour du point O.La barre est animée d’un mouvement de rotation complexe tel que :
1° Exprimer dans un repère adapté et en vous aidant du formulaire le vecteur vitesse en fonction de A, L et t. En déduire sa norme.
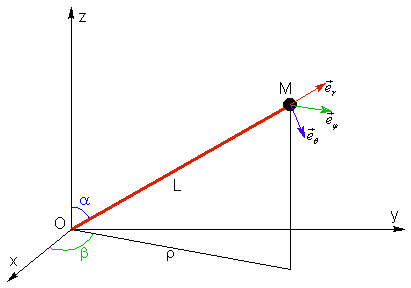
On choisi la base sphérique 
avec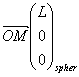 
avec L constant et on a :
; 
et 
; 
; 
; 
et
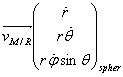devient avec les données de l’énoncé
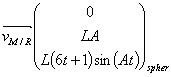
d’où la norme : 
2° Exprimer en vous aidant du formulaire le vecteur accélération en fonction de A,L et t.
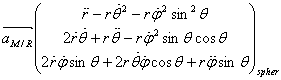devient avec les données de l’énoncé
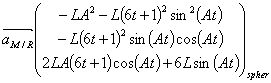
III) STATIQUE : L’échelle double 6 points
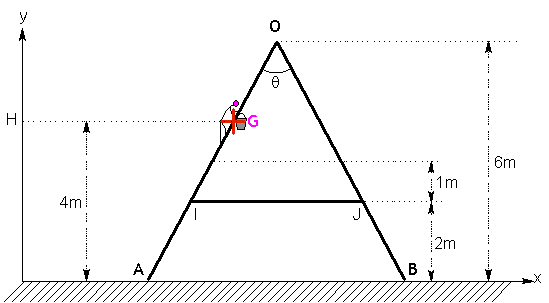
Considérons une échelle double constituée de deux échelles simples en aluminium de 20 kg chacune.
Les deux échelles sont liées par un axe parfait sans frottement en O et attachées en I et J par une corde.
La corde est de poids négligeable.
Le sol sur laquelle elle est posée est considéré comme parfaitement lisse et donc sans frottement.
Un homme muni d’un seau a son centre de masse G sur l’échelle à une hauteur de 4m, l’ensemble pesant 80kg.
On prendra pour simplifier g=10N/kg
Pour simplifier nos relations, on ne prendra pas en compte les forces s’exerçant en O.
L’angle q est de 60°.
1° Faire un bilan de forces s’exerçant sur l’échelle et compléter l’annexe en les faisant figurer. On explicitera les coordonnées des différentes forces dans le repère cartésien.
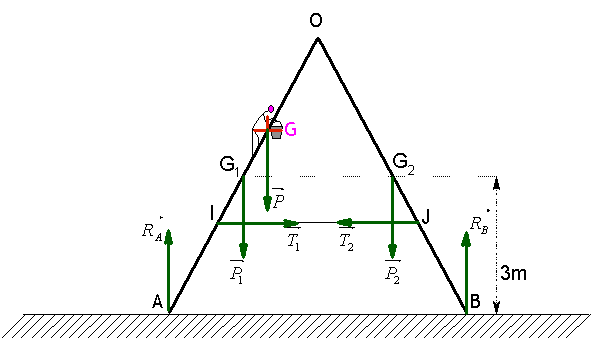
On a :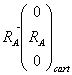
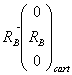
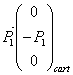
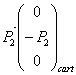
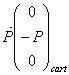
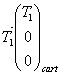
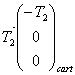
2° Rappeler les conditions d’équilibre des forces et des moments par rapport au point O
3° Exploiter ces conditions pour établir les équations que doivent satisfaire les forces.
On calculera
pour cela le moment vectoriel des forces par rapport au point O.( Rappel 
et donc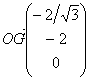 
)
● entraîne :
(u)
(v)
● entraîne :
on a :
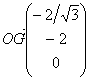
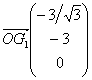
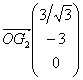
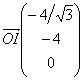
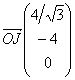
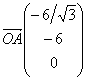
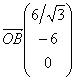
soit 
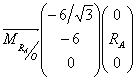et donc 
De même 
; 
; 
et 
soit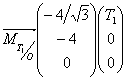 
et donc 
et aussi
soit 
(w)
4° En déduire les valeurs des réactions au sol.
De w et v on déduit : 
Avec les valeurs 
; 
on obtient le
système
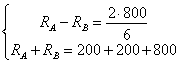
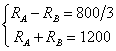
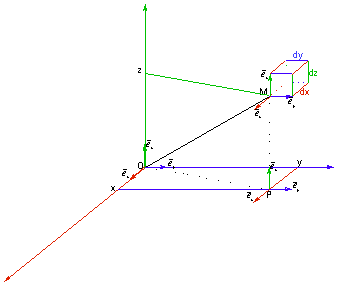
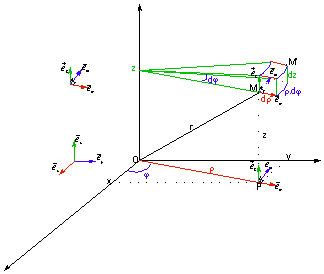
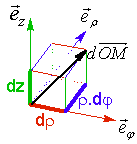
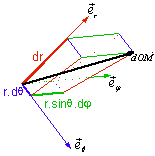
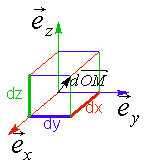Déplacement élémentaire :
Volume élémentaire :
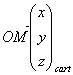
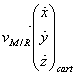
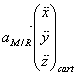
Déplacement élémentaire :
Volume élémentaire :
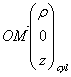
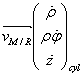
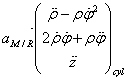
Déplacement élémentaire :
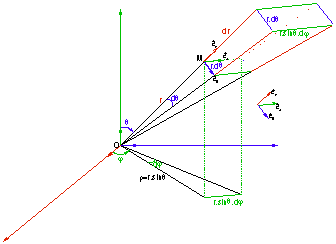
Volume élémentaire :
