Energétique

L’utilisation de grandeurs scalaires plutôt que vectorielles permet à la fois de simplifier les équations et d’avoir une meilleure compréhension des phénomènes aux travers de grandeurs plus intuitives : les grandeurs énergétiques.

2.5.1.1 Puissance, Travail et énergie potentielle

Puissance

Dans le cas simple d’un solide ponctuel la puissance d’une force correspond au produit scalaire de la force par la vitesse de déplacement de son point d’application :

Dans le cas d’une force F agissant sur un système de points on écrira :

- pour une distribution discrète :

Ce qui peut se simplifier en introduisant la notion de solide et les grandeurs torsorielles associées. La puissance s’obtient à l’aide du coproduit torsoriel :

qui correspond aux produits scalaires suivants :

où désigne la vitesse de translation du solide et sa vitesse angulaire de rotation.

Lorsque P sera positif, on parlera de puissance motrice tandis qu’on parlera de puissance résistante dans le cas contraire. L’unité de puissance est le Watt.

Travail

Le travail élémentaire d’un solide ponctuel correspond au produit de la force par le vecteur déplacement élémentaire :

Que l’on peut aussi écrire par référence à la vitesse :

Dans le cas d’un système de points soumis à une force F on écrira :

Ce qui se simplifie à l’aide des grandeurs torsorielles du solide par le coproduit torsoriel :

qui correspond aux produits scalaires suivants :

où désigne la vitesse de translation du solide et sa vitesse angulaire de rotation.

On notera bien que généralement le travail élémentaire est une forme différentielle et comme rappelé dans le §1.2, le travail W que l’on calculera ne dépendra pas uniquement des états initiaux et finaux du système mais aussi du ‘chemin’ parcouru entre ces états.

L’unité de travail est le Joule.

Energie potentielle

Dans certains cas, le travail peut se mettre sous la forme d’une différentielle totale exacte et il ne dépend alors que des états initiaux et finaux. On parle alors non plus de travail mais d’énergie potentielle :

On ne pourra définir cette grandeur que dans le cas de forces dites conservatives.

Ce qui s’écrira dans le cas d’un système de points :

et dans le cas du solide :

Inversement on pourra dire que ces forces dérivent d’un potentiel et on traduira cela mathématiquement par :

Entre deux états A et B, on pourra intégrer et calculer l’énergie potentielle :

Travail et énergie potentielle des forces usuelles

Le poids

On prend et donc .

Si l’on suppose que le solide est de masse constante et qu’il est placé dans un champ gravitationnel constant alors :

et donc définir une énergie potentielle élémentaire :

Soit par intégration :

Le poids est donc une force conservative et on notera le travail : et l’on peut par exemple calculer dans le cas de la chute libre d’un corps d’un point A de hauteur h_A au point B de hauteur h_B:

Travail résistant

Force de rappel d’un ressort

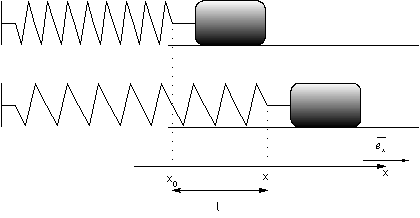
où k est la constante de raideur du ressort et avec on peut écrire :

et donc par intégration :

Comme précédemment la force de rappel est une force conservative et on aura le travail :

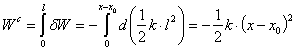
Il est à noter que l’intégration se fait sur l’allongement et non sur la position on n’a pas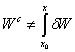

Force de frottement visqueux

Dans ce cas le travail dépend de la vitesse que prend le mobile entre les points A et B on aura :

et on ne peut définir d’énergie potentielle.

On dira que les forces de frottement sont non conservatives.

2.5.1.3 Energie cinétique

On a bâti précédemment une grandeur scalaire à partir du torseur force, on peut désormais faire de même avec le torseur cinétique.

Pour lui conserver son homogénéité avec une énergie et pouvoir utiliser le principe fondamental de la dynamique on défini l’énergie cinétique dans la cas du solide ponctuel par :

Soit :

Soit par intégration :

On prend comme constante la valeur nulle pour avoir une énergie cinétique nulle à vitesse nulle.

Dans le cas d’une distribution discrète de points on notera :

et d’une distribution continue :

Et en utilisant la notation plus simple des torseurs, l’énergie cinétique sera pour le solide

soit par intégration :

où C désigne le centre de masse du solide.

Dans le cas d’un mouvement de translation on aura :

et d’un mouvement de rotation :

2.5.1.4 Energie mécanique

On appellera énergie mécanique, la somme de l’énergie due au mouvement () et de l’énergie due aux forces conservatives :

Il est à noter que dans le cas d’un solide soumis à des forces intérieures et extérieures, l’énergie mécanique s’écrit en détaillant :

Cette remarque prend toute son importance dans l’application du théorème de l’énergie mécanique.

2.5.1.5 Energie totale

On appellera énergie totale, la somme de toutes les formes d’énergie d’un solide et on le notera.

On pourra décomposer cette énergie en deux types :

- les grandeurs énergétiques mesurables de la mécanique :

- l’énergie cinétique du solide

- l’énergie potentielle des forces extérieures.

- toutes les autres :

- l’énergie interne U (qui comprend l’énergie potentielle des forces intérieures).

2.5.2 Théorèmes mathématiques

2.5.2.1 Transport des moments

Calculons le moment en deux points différent O et O’ :

et de même on aurai avec le moment cinétique :

2.5.2.2 Référentiel du centre de masse

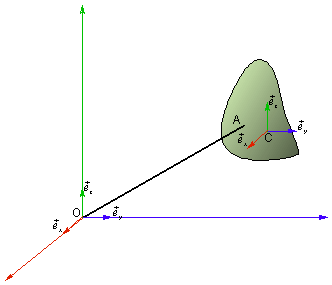
Afin de simplifier certaines expressions, il est intéressant de définir un référentiel particulier appelé référentiel du centre de masse et noté R_c. Ce référentiel en translation par rapport au référentiel d’étude est tel que dans ce référentiel attaché au solide, sa résultante cinétique soit nulle.

on a vu en 1.4.5.1 que le centre d’inertie du solide se défini par:

et donc 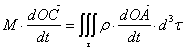soit

dans le référentiel du centre de masse on aura

On retiendra que le centre de masse C est fixe dans ce référentiel défini par

2.5.2.3 Théorème de Koenig

Théorème de Koenig pour le moment cinétique

Utilisons pour démontrer ce théorème le moment cinétique d’une distribution continue de masse M.

Exprimons le moment cinétique dans R par rapport à O

Exprimons le moment cinétique dans R_C par rapport à C (point fixe de R_C) :

Le référentiel R_C étant en translation par rapport à R on a :

que l’on insère dans le moment cinétique :

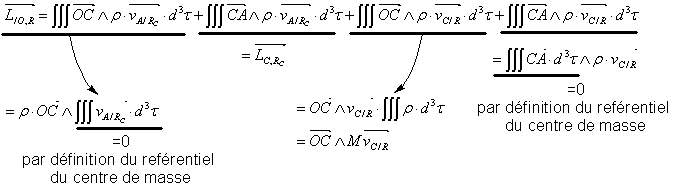
Ce théorème qui se rapporte à un point fixe permet l’application plus aisée du théorème du moment cinétique.

Théorème de Koenig pour l’énergie cinétique

Avec de même que précédemment :

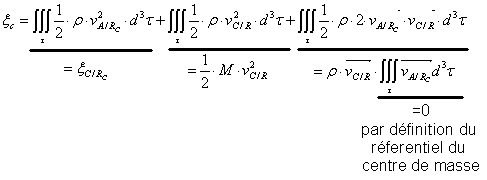
2.5.3 Théorème de l’énergie cinétique

Le théorème de l’énergie cinétique correspond à la mise en relation des grandeurs énergétiques au travers du principe fondamental de la dynamique.

en multipliant par [v] :

ou encore en intégrant :

Le théorème s’énonce ainsi :

La variation d’énergie cinétique d’un solide correspond au travail des forces s’appliquant sur ce solide.

Remarques importantes :

● Lorsque l’on a énoncé le principe fondamental de la dynamique on a fait apparaître uniquement les forces extérieures car la somme des forces intérieures ainsi que la somme des moments des forces intérieures étaient nulles. Mais dans le théorème de l’énergie cinétique, le fait d’appliquer un produit scalaire avec la vitesse de chaque point du solide n’entraîne pas la nullité de la somme. Ainsi le théorème de l’énergie cinétique prend en compte des forces qui n’apparaissent pas dans le théorème fondamental de la dynamique. On peut donc écrire :

● Il faut noter d’autre part que le travail désigne un transfert d’énergie et non une énergie. Ce transfert d’énergie correspond à la variation de l’énergie cinétique. Par contre, on peut dire qu’à tout instant le solide possède une énergie cinétique, ce qui n’est pas le cas avec le travail.

2.5.3 Théorème de l’énergie mécanique

L’intérêt de définir l’énergie mécanique et par la même d’utiliser un théorème de l’énergie mécanique est de faire apparaître une distinction entre forces conservatives et non conservatives.

En effet :

D’après le théorème de l’énergie cinétique :

et par définition de l’énergie potentielle on a :

Soit :

Ainsi en l’absence de forces ne dérivant pas d’un potentiel l’énergie se conserve :

D’où l’appellation de conservative pour les forces dérivant d’un potentiel.

2.5.5 Transferts énergétiques

2.5.5.1 Différents types de transfert

On vient de voir que le travail noté W correspondait à un transfert d’énergie. Si l’on regarde un peu plus précisément le comportement des particules élémentaires qui subissent un travail, on s’aperçoit que leurs niveaux d’énergie varient mais que leur répartition dans ces niveaux énergétiques reste inchangée. C’est pourquoi on dit que le travail correspond à un transfert d’énergie macroscopique.

Par opposition, on définira un transfert d’énergie microscopique qui au sein des particules élémentaires se traduira par une modification non pas des niveaux d’énergie mais de la répartition des particules dans ceux-ci. Ces transferts sont nommés transfert calorique ou chaleur et noté Q

Ainsi défini il n’existe que deux types de transferts énergétiques :

- Le travail W : transfert d’énergie macroscopique,

- La chaleur Q : transfert d’énergie microscopique.

Le travail n’est pas forcément clairement associé à une force. Par exemple le travail électrique d’une résistance R sera

Qu’ils soient macroscopiques ou microscopiques, les transferts d’énergie se font sous plusieurs modes qui seront détaillés dans la suite du cours (par M^r Dounies):

- les transferts radiatifs dû aux photons et appelé rayonnement,

- les transferts convectifs dû à un mouvement d’ensemble de la matière.

- les transferts diffusifs dû aux mouvements d’agitation de la matière et appelé conduction.

2.5.5.2 Premier principe de thermodynamique

Les principes qui régissent les lois de la physique sont peu nombreux. Après avoir énoncé les principes fondamentaux de la mécanique, voici le premier principe de thermodynamique :

Pour tout système n’échangeant avec l’extérieur que de l’énergie on a :

où W et Q désignent les transferts d’énergie à travers la surface délimitant le système.

On pourra aussi écrire

2.5.5.3 Rendement

On définira le rendement comme le rapport :