Cours de statique et de dynamique
![]()
http://convergence.chez.tiscali.fr/phys/sup/meca/
2.3 Notions de forces et d’équilibre
2.3.2 Equilibre, rotation et translation
2.3.2.2 Couple et mouvement de rotation
2.3.4 Résolution des problèmes de statique
2.3.4.1 Solide en équilibre sous l’action de 2 forces
2.3.4.2 Solide en équilibre sous l’action de 3 forces
2.3.4.3 Solide en équilibre sous l’action de n forces
2.4.1.1.1 Quantité de mouvement
2.4.1.1.3 Arrêt, rotation et translation.
2.4.2 Principes fondamentaux de la dynamique
2.4.2.2 Enoncé mathématique du principe fondamental
2.4.2.3 Théorème de la quantité de mouvement, Théorème de la résultante cinétique
2.4.2.4 Théorème du moment cinétique
2.4.3 Dynamique des particules chargées
2.4.3.2 Particule dans un champ électrique.
2.4.3.3 Particule dans un champ magnétique
2.3 Notions de forces et d’équilibre
Toute action mécanique s’exerçant sur un objet a pour effet soit :
- de modifier son mouvement ou de le mettre en mouvement,
- de le maintenir en équilibre,
- de le déformer.
Toute action mécanique peut être décrite par une somme d’actions élémentaires.
Toute action mécanique élémentaire s’exerçant sur un corps peut être décrite par la connaissance des quatre caractéristiques suivantes :
- le point d’application,
- la droite d’action,
- le sens,
- la valeur : son intensité.
Ces quatre caractéristiques sont celles d’un vecteur lié.
La connaissance de ces quatre caractéristiques permet de construire une grandeur vectorielle nommée force.
La connaissance de l’ensemble de ces caractéristiques représentant l’ensemble des actions élémentaires permettra de décrire le solide à n’importe quel instant. C’est dans cette hypothèse déterministe que nous nous placerons dans l’ensemble de ce cours.
Il est important de noter qu’une action sur un solide le mettant ou modifiant son mouvement peut être décrite par un ensemble de forces mais que la simple connaissance de la somme de ces forces (somme vectorielle) n’est pas suffisante pour en décrire le mouvement. Il est alors nécessaire de connaître une grandeur supplémentaire qu’est le moment total des forces (somme vectorielle des moments des forces) s’exerçant sur le solide. En effet une somme de forces nulle peut très bien mettre en mouvement un solide.
Pour être complet dans la connaissance d’une action il faudra donc connaître deux grandeurs :
- la somme vectorielle des forces s’exerçant sur le solide.
- la somme vectorielle des moments des forces s’exerçant sur le solide.
On retiendra donc que pour décrire le mouvement d’un solide dans l’espace, il nous faudra connaître le couple suivant [Somme des forces, Somme des moments des forces] nommé Torseur force et noté [F].
Ainsi les équations de la dynamique exprimées sur les forces et sur les moments pourront être ramenées à des équations torsorielles.
A chaque action élémentaire, on associera un torseur composé du vecteur force et de son moment.
Il est à noter que le moment permet de décrire la mise en rotation d’un solide. C’est pourquoi pour une première approche de la dynamique si on se limite à l’étude d’un point ou du centre d’inertie d’un solide l’utilisation des torseurs est inutile et la seule connaissance des vecteurs forces suffit, laissant de côté la notion de moment. Mais dans l’étude de la mécanique du point, il ne faut pas oublier que l’on perd une partie de la généralité.
2.3.1 Le torseur force
2.3.1.1 Les forces
Les forces peuvent être regroupées en trois familles :
- Les forces de champ : force de gravitation, force de Lorentz
- Les forces de contact : force de frottement,…
- Les forces nucléaires assurant la cohésion du noyau atomique.
Les forces s’expriment en Newton noté N
Le poids qui appartient à la première famille est défini par les caractéristiques suivantes :
- Point d’application : le centre d’inertie du solide
- Droite d’action : la verticale
- Sens : Vers le bas
- Valeur : P=mg avec m masse en kg du solide et g=9,81N/kg sur terre
Dans le cas des forces de contact le point d’application correspond au point de contact.
2.3.1.2 Moment de forces
Le moment total des forces est la grandeur qui va nous permettre de savoir si l’action aura pour effet la mise en rotation du solide.
Il s’exprime en un point O quelconque et pour une force ![]() ayant
A comme point d’application par :
ayant
A comme point d’application par :
![]()
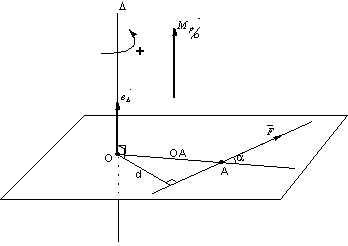
Le moment est un vecteur libre.
Il est indépendant de la position de A sur la droite d’action.
Norme du moment :![]()
Pour des raisons de simplification, si le solide est en rotation autour d’un axe, on préférera généralement exprimer le moment par rapport à cet axe. Avec O passant par l’axe de rotation D on a :
![]()
![]() est la projection de
est la projection de ![]() sur l’axe D de vecteur directeur
sur l’axe D de vecteur directeur ![]() .Le scalaire
.Le scalaire![]() est
indépendant du choix de O sur l’axe D.
est
indépendant du choix de O sur l’axe D.
Se choisir un vecteur ![]() c’est choisir un sens positif pour
la rotation autour de l’axe D. Le signe
du moment par rapport à l’axe est donc positif si la rotation du vecteur
c’est choisir un sens positif pour
la rotation autour de l’axe D. Le signe
du moment par rapport à l’axe est donc positif si la rotation du vecteur ![]() autour
de D se fait dans le sens positif
choisi.
autour
de D se fait dans le sens positif
choisi.
2.3.2 Equilibre, rotation et translation
 2.3.2.1
Equilibre
2.3.2.1
Equilibre
Tout mouvement d’un solide dans l’espace peut être décomposé en :
- un mouvement de translation et
- un mouvement de rotation.
La connaissance de la somme des forces s’exerçant sur un solide renseignera sur la modification de son mouvement de translation. Ce vecteur indiquant le sens et la direction du mouvement. L’absence de translation se traduisant par une somme de forces nulle.
La connaissance de la somme des moments des forces
s’exerçant sur un solide renseignera sur la modification de son mouvement de
rotation. En effet toute force ![]() ayant A comme point d’application
s’appliquant sur un solide dont l’axe de rotation passe par le point O mettra
ce solide en rotation autour de son axe tant que le vecteur
ayant A comme point d’application
s’appliquant sur un solide dont l’axe de rotation passe par le point O mettra
ce solide en rotation autour de son axe tant que le vecteur ![]() ne sera pas
colinéaire au vecteur force
ne sera pas
colinéaire au vecteur force ![]() . La rotation s’arrêtant quand les
vecteurs sont colinéaires soit le produit vectoriel nul.
. La rotation s’arrêtant quand les
vecteurs sont colinéaires soit le produit vectoriel nul.


Un solide ne pourra être maintenu dans son état d’équilibre que s’il n’est mis ni en translation ni en rotation.
Cela se traduit mathématiquement par :
![]() et
et ![]()
ou plus synthétiquement par le torseur force [F] :
![]()
 2.3.2.2
Couple et mouvement de rotation
2.3.2.2
Couple et mouvement de rotation
Un solide dont la somme des forces est nulle mais le moment total non nul est soumis à un couple.
![]()
![]()
Un couple est une action qui met le solide uniquement en rotation.
Un solide initialement en translation et soumis à un couple restera en translation mais subira en plus un mouvement de rotation
2.3.2.3 Translation
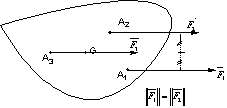 La modification du mouvement d’un solide, soumis à un
ensemble de forces non nulles mais de moment total nul, sera une translation.
La modification du mouvement d’un solide, soumis à un
ensemble de forces non nulles mais de moment total nul, sera une translation.
![]()
![]()
Un solide initialement en rotation et soumis à une somme de force non nulle mais de moment total nul restera en rotation mais subira en plus un mouvement de translation.
2.3.3 Forces de frottement
Réaction du support et force de frottement sont généralement
inclues dans une même force notée![]() . Le torseur
. Le torseur ![]() se décompose
donc en :
se décompose
donc en :
![]() :
Réaction
normale
:
Réaction
normale
![]() :
Moment de résistance au pivotement
:
Moment de résistance au pivotement
![]() :
Réaction tangentielle = force de
frottement
:
Réaction tangentielle = force de
frottement ![]() :
Moment de résistance au roulement
:
Moment de résistance au roulement
2.3.3.1 Frottement statique
Quand le solide est immobile du fait des frottements on peut définir un facteur de frottement statique µS.
µs est défini à partir de la valeur maximale que peut prendre la composante tangentielle sans qu’il y ait de mouvement.
On a donc ![]() et donc quand le solide est
immobile :
et donc quand le solide est
immobile : ![]()
On peut aussi utiliser l’angle de frottement statique et le cône de frottement pour mieux visualiser la limite à partir de laquelle le solide va glisser.
A partir du moment où ![]() est supérieur à
est supérieur à ![]() , le solide
se met en mouvement et il faut utiliser le facteur de frottement dynamique µD.
, le solide
se met en mouvement et il faut utiliser le facteur de frottement dynamique µD.
2.3.3.2 Frottement dynamique
Le facteur de frottement dynamique µD qui comme µS est une grandeur tabulée qui dépend de la nature du contact, permet d’exprimer la composante tangentielle en fonction de la composante normale :
![]()
La valeur de µD est obligatoirement inférieure à µS
Exemple : Solide sur un plan incliné
Prenons un solide de poids P=100N posé sur un plan incliné d’un angle a.
Le solide est en équilibre si les deux forces ![]() et
et ![]() sont
égales et opposées.
sont
égales et opposées.
On suppose ![]() et
et ![]() .
. ![]()
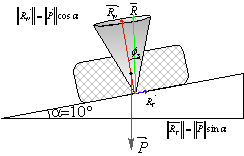
Tant que la pente est d’angle ![]() , la réaction vaut
, la réaction vaut ![]() et la force
de frottement
et la force
de frottement ![]() ce qui est vérifie
ce qui est vérifie ![]() , on dit que la
réaction est dans le cône de frottement statique :
, on dit que la
réaction est dans le cône de frottement statique :
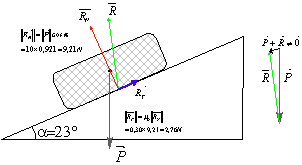
Mais dès que l’angle ![]() on a toujours
on a toujours ![]() mais la valeur
mais la valeur ![]() est
supérieure à
est
supérieure à ![]() donc on calcule désormais
donc on calcule désormais ![]() car le
solide se met à glisser.
car le
solide se met à glisser.
2.3.4 Résolution des problèmes de statique
2.3.4.1 Solide en équilibre sous l’action de 2 forces
Pour qu’un solide soit en équilibre sous l’action de 2 forces, il faut et il suffit que les deux forces soient égales et directement opposées.
2.3.4.2 Solide en équilibre sous l’action de 3 forces
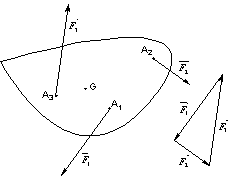
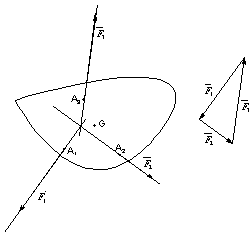
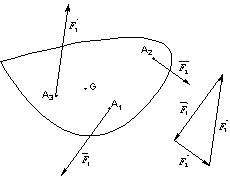
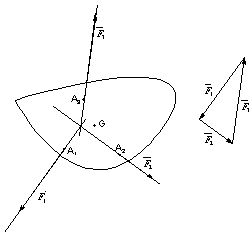
Pour qu’un solide soit en équilibre sous l’action de 3 forces, il faut et il suffit que :
- les 3 forces soient coplanaires.
- les 3 forces soient concourantes au même point.
- chacune des forces soit opposée à la somme géométrique des 2 autres : dynamique fermé.
2.3.4.3 Solide en équilibre sous l’action de n forces
Propriété très importante :
La projection sur un plan d’un système de n forces en équilibre est un systèmes de n forces coplanaires en équilibre.
Pour les corps possédant un plan de symétrie ce plan sera toujours choisi comme plan de projection.
2.3.4.4 Méthode
Pour résoudre un problème de statique il faut procéder généralement ainsi :
- Réaliser un dessin de situation où figure le système à étudier dans son environnement extérieur sans y faire figurer de forces.
- Réaliser un dessin où ne figure que le système étudié et les forces extérieures qu’il subit.
- Faire un bilan des caractéristiques connues et inconnues des forces.
- Réaliser la construction mathématique traduisant les conditions d’équilibre : le dynamique des forces.
- Exploiter ces différentes étapes pour résoudre le problème.
L’utilisation du moment par rapport à un axe donne une équation :
![]()
Et l’utilisation de la projection de la somme vectorielle des forces sur un plan (Oxy) en fournit deux autres :
![]()
![]()
2.4 Dynamique des solides
La dynamique est la partie de la mécanique qui étudie les causes du mouvement.
2.4.1 Eléments de dynamique
Pour qui a bien compris que tout mouvement pouvait se construire à partir d’un mouvement de translation et de rotation, a compris la nécessité des torseurs. Cette entité composée de deux vecteurs traduisant le mouvement de translation et de rotation a été introduite avec les forces. C’est désormais avec les éléments cinétiques que nous allons le définir.
2.4.1.1 Le torseur cinétique
Le torseur cinétique [P] correspond aux grandeurs [quantité de mouvement, moment cinétique] décrites ci-après.
Il est important de noter que ces grandeurs dépendent du référentiel choisi.
2.4.1.1.1 Quantité de mouvement
Pour étudier le mouvement d’un solide ponctuel isolé, on pourrait se contenter de connaître sa vitesse. Mais l’étude du mouvement de deux solides en interaction ne pourra se faire que par la pondération des vitesses par une grandeur qui dépend de l’objet. Cette grandeur est appelée masse inerte (inerte : inertie : vitesse).
L’expérience montre que cette grandeur qui pondère la vitesse d’un solide est la même que celle qui pondère la force gravitationnelle des solides entre eux et nommée masse grave. On nommera donc masse sans distinction la masse grave et la masse inerte.
Aussi on va utiliser un vecteur ![]() qui correspond à la
pondération de la vitesse par cette grandeur appelée masse :
qui correspond à la
pondération de la vitesse par cette grandeur appelée masse :
![]()
![]() est appelée quantité
de mouvement.
est appelée quantité
de mouvement.
Lorsque le solide n’est pas ponctuel il faudra utiliser la résultante cinétique :
![]()
2.4.1.1.2 Moment cinétique
Dans le cas d’un solide quelconque, il faudra en plus de la résultante cinétique du solide définir le moment total associé appelé moment cinétique résultant :
![]()
Dans le cas d’une distribution non pas discrète mais continue on calculera
![]() et
et ![]()
2.4.1.1.3 Arrêt, rotation et translation.
Par analogie avec le torseur force où l’on avait défini les 3 cas : équilibre, couple et translation on peut écrire les 3 cas suivant :
- Le solide
est à
l’arrêt :
![]() et
et
![]()
- Le solide
est en
rotation :
![]() et
et
![]()
- Le solide
est en translation :
![]() et
et
![]()
2.4.1.1 Le torseur dynamique
Lorsque la vitesse varie on utilise l’accélération pour décrire cette variation. De la même façon on peut définir un torseur dynamique [D] à partir de la quantité d’accélération et du moment dynamique. Et pour un solide on prendra la résultante dynamique et le moment dynamique résultant :
![]()
![]()
![]() et
et ![]()
2.4.2 Principes fondamentaux de la dynamique
2.4.2.1 Enoncés de Newton
Première loi : Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme, sauf si des forces imprimées le contraignent d’en changer.
Deuxième loi : Le changement de mouvement est proportionnel à la force imprimée et s’effectue suivant la droite par laquelle cette force est imprimée.
Troisième loi : La réaction est toujours contraire à l’action : ou encore les actions que deux corps exercent l’un sur l’autre sont toujours égales et dirigées en sens contraire.
2.4.2.2 Enoncé mathématique du principe fondamental
Ce principe issu de la deuxième loi de Newton rend équivalent deux grandeurs fondamentalement différentes en liant le mouvement aux forces.
Dans un référentiel galiléen R, le mouvement d’un système de points matériels par rapport à un point fixe O de R vérifie l’équation torsorielle suivante :

en notant ![]() le torseur des forces extérieures
dont le moment est calculé par rapport à O.
le torseur des forces extérieures
dont le moment est calculé par rapport à O.
En extrayant du torseur ses deux composantes vectorielles, on obtient les deux théorèmes suivants.
2.4.2.3 Théorème de la quantité de mouvement, Théorème de la résultante cinétique
Dans le cas d’un solide ponctuel on obtient le théorème de la quantité de mouvement :
![]()
Dans le cas d’un solide non ponctuel on parle de théorème de la résultante cinétique.
2.4.2.4 Théorème du moment cinétique
Le théorème liant les moments s’exprime par :
![]()
Ce théorème peut s’avérer utile même lorsque la résultante du moment des forces est nulle car le moment cinétique est alors une constante vectorielle. Mais on l’utilisera surtout pour l’étude des solides et non pour l’étude de la dynamique du point.
2.4.3 Dynamique des particules chargées
Ce chapitre de dynamique se place d’emblé dans un cadre restreint d’étude des particules.
Celles-ci sont considérées comme ponctuelles, oubliant ainsi la possibilité d’une éventuelle rotation de la particule sur elle-même et restreignant l’étude à un problème de dynamique du point.
Leurs vitesses sont supposées très inférieures à la vitesse de la lumière pour rester dans le cadre de la mécanique newtonienne.
2.4.3.1 Forces de champ
Les particules chargées possèdent deux caractéristiques intrinsèques : leur masse m et leur charge q, et la caractéristique de mouvement : leur vitesse v.
Champ gravitationnel :
C’est dans un champ gravitationnel ![]() qu’apparaît la force
de gravitation :
qu’apparaît la force
de gravitation :
![]()
Avec le champ ![]() créé par une distribution volumique
de masse
créé par une distribution volumique
de masse ![]() qui
à la distance r de la particule vaut :
qui
à la distance r de la particule vaut :
![]()
Champ électromagnétique :
C’est dans un champ électromagnétique ![]() qu’apparaît la force
de Lorentz :
qu’apparaît la force
de Lorentz :
![]()
L’étude sur terre d’une particule telle que l’électron de
masse ![]() et
de charge
et
de charge ![]() et de vitesse
et de vitesse ![]() soumis aux
champs habituels:
soumis aux
champs habituels:
![]() ,
,![]() et
et![]()
met en concurrence :
- une force gravitationnelle ![]()
- une force de Lorentz ![]()
La force de Lorentz est alors dix mille milliards (1013) de fois plus intense que la force gravitationnelle.
On négligera donc généralement la force gravitationnelle devant la force de Lorentz.
2.4.3.2 Particule dans un champ électrique.
 Soit la particule de charge q initialement prise à
l’origine du repère, de masse m, de vitesse
Soit la particule de charge q initialement prise à
l’origine du repère, de masse m, de vitesse 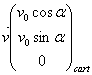 et soumis au champ
électrique
et soumis au champ
électrique ![]() tel que
tel que ![]() .
.
L’application du théorème de la quantité de mouvement donne :
![]()
soit :
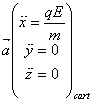
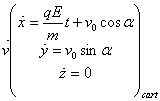
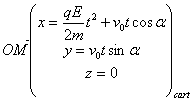
D’où l’équation de la trajectoire :
![]()
On peut dégager deux cas particuliers :
a=0 :
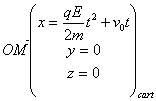
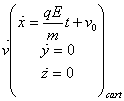
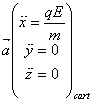
Il s’agit d’un mouvement rectiligne uniformément varié dans le sens du champ
a=π/2 :
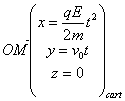
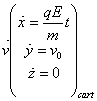
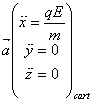
L’équation de la trajectoire est alors : ![]() qui est
l’équation d’une parabole d’axe Ox.
qui est
l’équation d’une parabole d’axe Ox.
Il s’agit d’un mouvement parabolique uniformément varié.
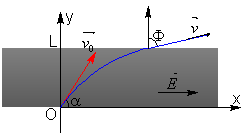 Si le champ électrique n’est que sur une hauteur L on
obtient :
Si le champ électrique n’est que sur une hauteur L on
obtient :
![]() et
et 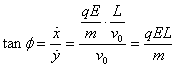
soit ![]() ou
ou ![]()
2.4.3.3 Particule dans un champ magnétique
Soit la particule de charge q initialement prise à l’origine
du repère, de masse m, de vitesse 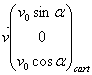 et soumis au champ magnétique
et soumis au champ magnétique ![]() tel
que
tel
que ![]() .
.
L’application du théorème de la quantité de mouvement donne :
![]()
![]()
Posons![]() , on a
, on a 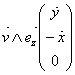 soit :
soit : 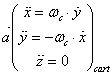 et par
intégration
et par
intégration 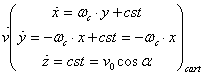
En réintroduisant l’expression ![]() dans l’expression de
dans l’expression de ![]() on obtient
l’équation différentielle :
on obtient
l’équation différentielle :
![]()
Comme indiqué au paragraphe 1.3.1 cette équation a pour
solutions : 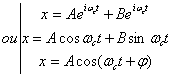
Les conditions initiales donnent à t=0 :
![]() et
et ![]()
Or en prenant ![]() comme type de solution on a à t=0
comme type de solution on a à t=0
![]() et
et ![]()
Ce qui permet de trouver les constantes ![]() et
et ![]() or
or ![]() d’où
d’où
![]()
![]() ce qui donne par intégration
ce qui donne par intégration ![]()
Les conditions initiales donnent à t=0 ![]() :
:
![]()
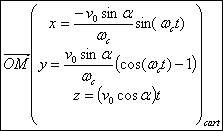
On reconnaît le vecteur position d’un mouvement
hélicoïdal (cf TD1) de pas d’hélice ![]() et de rayon
et de rayon![]() .
.