Mécanique au Bac PRO
http://convergence.chez.tiscali.fr
Vocabulaire :
Repères d’espace :
L’ensemble constitué d’un point O de l’espace et de 3 vecteurs de base forme un repère d’espace.
Repère de Copernic :
L’origine correspond au centre de masse du système solaire et les axes sont dirigés vers trois étoiles fixes.
Repère géocentrique :
L’origine correspond au centre de masse de la terre et les axes sont dirigés vers trois étoiles fixes.
Coordonnées :
Pour définir la position de tout point dans un repère, on constate expérimentalement, qu’il est nécessaire et suffisant de prendre trois réels appelés coordonnées.
Repère de temps
Il est constitué d’un instant d’origine et d’une échelle de temps
Référentiel
L’ensemble constitué d’un repère d’espace et d’un repère de temps est appelé référentiel.
Référentiel galiléen :
C’est un référentiel dans lequel l’espace est homogène et isotrope et le temps uniforme.
Cinématique
Position d’un point
Un point M dans un repère R est caractérisé par son vecteur position :
![]()
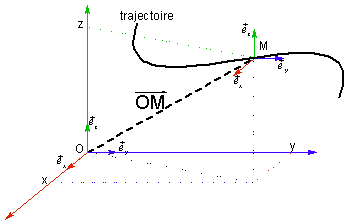
En coordonnées cartésiennes on note :
![]()
![]() ou
ou
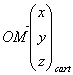
où indique que les coordonnées du vecteur sont celles qu’il a dans la base cartésienne.
La trajectoire étant l’ensemble des positions occupées par le point M.
L’équation de la trajectoire du point M est la relation liant les coordonnées indépendamment du temps.
On appelle équation horaire l’expression des coordonnées du point en fonction du temps :
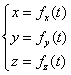
Si le mouvement est plan, on choisit le repère de telle sorte que deux coordonnées suffisent. Généralement on conserve les coordonnées x et y.
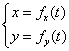
Si le mouvement est rectiligne, on choisit le repère de telle sorte qu’une seule coordonnée suffise. Généralement on conserve la coordonnée x.
![]()
Vitesse d’un point
La vitesse moyenne v d’un point est obtenue en calculant le rapport de la distance parcourue d par la durée du parcours t :
![]()
Lorsque l’on veut obtenir le vecteur vitesse moyenne entre deux points M1(t1) et M2(t2)on exprime :
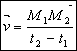
Si l’on veut exprimer le vecteur vitesse instantanée en un point M de la trajectoire il faut faire le calcul :
![]()
Le vecteur exprimé est celui de la vitesse du point M dans son mouvement par rapport au référentiel R.
En coordonnées cartésiennes (base fixe) le mouvement du point M par rapport au référentiel cartésien donne le vecteur vitesse noté:
![]() ou
ou
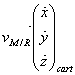
On notera les points suivants :
● ![]() désigne la
dérivée de
désigne la
dérivée de ![]() soit
soit
![]()
● ![]() désigne la
dérivée de
désigne la
dérivée de ![]() soit
soit
![]()
● ![]() désigne la
dérivée de
désigne la
dérivée de ![]() soit
soit
![]()
● L’unité légale de la vitesse est le mètre par seconde m/s ou m.s-1
● Le vecteur vitesse en un point est confondu à la tangente à la trajectoire en ce point.
● Le sens du vecteur vitesse est celui du mouvement.
● Comme pour tout vecteur la norme de la vitesse correspond à la racine carrée de la somme du carré des composantes de ce vecteur.
![]()
Accélération d’un point
De même que pour la vitesse on peut définir les vecteurs accélération moyenne et accélération instantanée.
Le vecteur accélération moyenne est obtenu entre deux vecteurs vitesses à des instants t1 et t2
![]()
Le vecteur accélération instantanée correspond à la dérivée du vecteur vitesse par rapport au temps :
![]() ou
ou
![]()
En coordonnées cartésiennes (base fixe) le mouvement du point M par rapport au référentiel cartésien donne le vecteur accélération noté :
![]() ou
ou
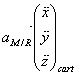
On notera les points suivants :
● L’unité légale de l’accélération est le mètre par seconde au carré m.s-2
Etude de mouvements
Types de mouvements
Dans le référentiel considéré.
La trajectoire peut être :
- rectiligne : - la trajectoire est une droite,
- circulaire : - la trajectoire est un cercle,
- la trajectoire est donc plane,
- curviligne : - la trajectoire est une courbe.
- hélicoïdale : - la trajectoire est une hélice.
- cycloïdale : - la trajectoire est une cycloïde.
Le mouvement peut être :
- uniforme : - la valeur algébrique de la vitesse est constante,
- le vecteur vitesse n’est pas forcément constant,
- uniformément varié : - la valeur algébrique de l’accélération est constante.
- accéléré : - la valeur algébrique de la vitesse augmente,
- ralenti : - la valeur algébrique de la vitesse diminue,
- sinusoïdal : - une composante de position dépend sinusoïdalement du temps.
Le mouvement d’un solide peut être :
- de translation : - le vecteur vitesse est identique en tout point du solide.
- de rotation : - la trajectoire de chaque point du solide est circulaire.
Par exemple la nacelle d’une grande roue a au démarrage un mouvement de translation circulaire uniformément varié
Exercice 1 : La voiture
Une voiture lancée sur une ligne droite à 72 km.h-1 s’arrête d’un mouvement uniformément varié en 8s.
 a) Indiquer la vitesse au début et à la fin
du mouvement.
a) Indiquer la vitesse au début et à la fin
du mouvement.
b) En déduire la déccélération
Exercice 2 : La valve
Sur une pente d’angle a=10°,
le cycliste descend avec une vitesse constante de 20 ![]() .
.
a) Par rapport à la route quelle est la nature de la trajectoire de l’axe du pédalier et de la valve située à la circonférence du pneu.
b) Calculer sa vitesse en km/h.
c) Indiquer la valeur de son accélération.
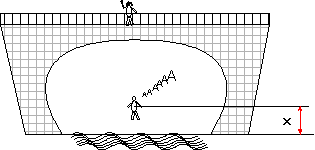 d) En combien de temps parcourt-il ½ km ?
d) En combien de temps parcourt-il ½ km ?
Exercice 3 : Le plongeur
L’accélération d’un plongeur sautant du haut d’un pont poussé par quelqu’un
vérifie : ![]()
a) Donner sa position au départ (t=0). En déduire la hauteur du pont.
b) Donner l’expression de sa vitesse à une date quelconque (il faut dériver).
c) Donner sa vitesse au départ.
d) Combien de temps met-il pour arriver dans l’eau (équation du second degré).
e) En déduire sa vitesse à l’arrivée dans l’eau.
f) Quelle est son accélération ? A quoi correspond cette valeur ?
g) Quelle est la nature du mouvement ?
Notions de forces et d’équilibre
Toute action mécanique s’exerçant sur un objet a pour effet soit :
- de modifier son mouvement ou de le mettre en mouvement,
- de le maintenir en équilibre,
- de le déformer.
Toute action mécanique peut être décrite par une somme d’actions élémentaires.
Toute action mécanique élémentaire s’exerçant sur un corps peut être décrite par la connaissance des quatre caractéristiques suivantes :
- le point d’application,
- la droite d’action,
- le sens,
- la valeur : son intensité.
Ces quatre caractéristiques sont celles d’un vecteur.
La connaissance de ces quatre caractéristiques permet de construire une grandeur vectorielle nommée force.
La connaissance de l’ensemble de ces caractéristiques représentant l’ensemble des actions élémentaires permettra de décrire le solide à n’importe quel instant.
Il est important de noter qu’une action sur un solide le mettant ou modifiant son mouvement peut être décrite par un ensemble de forces mais que la simple connaissance de la somme de ces forces (somme vectorielle) n’est pas suffisante pour en décrire le mouvement. Il est alors nécessaire de connaître une grandeur supplémentaire qu’est le moment total des forces (somme des moments des forces) s’exerçant sur le solide. En effet une somme de forces nulle peut très bien mettre en mouvement un solide.
Pour être complet dans la connaissance d’une action il faudra donc connaître deux grandeurs :
- la somme vectorielle des forces s’exerçant sur le solide.
- la somme des moments des forces s’exerçant sur le solide.
On retiendra donc que pour décrire le mouvement d’un solide dans l’espace, il nous faudra connaître le couple suivant [Somme des forces, Somme des moments des forces] nommé Torseur force et noté [F].
A chaque action élémentaire, on associera un torseur composé du vecteur force et de son moment.
Le torseur force
Les forces
Les forces peuvent être regroupées en trois familles :
- Les forces de champ : force de gravitation (le poids), force de Lorentz (force électromagnétique)
- Les forces de contact : force de frottement,…
- Les forces nucléaires assurant la cohésion du noyau atomique.
Les forces s’expriment en Newton noté N
Le poids qui appartient à la première famille est défini par les caractéristiques suivantes :
- Point d’application : le centre d’inertie du solide
- Droite d’action : la verticale
- Sens : Vers le bas
- Valeur : P=mg avec m masse en kg du solide et g=9,81N/kg sur terre
Dans le cas des forces de contact le point d’application correspond au point de contact.
Moment de forces
Le moment total des forces est la grandeur qui va nous permettre de savoir si l’action aura pour effet la mise en rotation du solide.
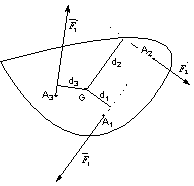 Si le solide est en rotation autour d’un axe D.
Avec d distance entre la droite d’action de la force et l’axe de rotation
on a :
Si le solide est en rotation autour d’un axe D.
Avec d distance entre la droite d’action de la force et l’axe de rotation
on a :
![]()
Dans l’exemple ci-contre on a les moments suivants :
![]()
![]()
![]()
Equilibre, rotation et translation
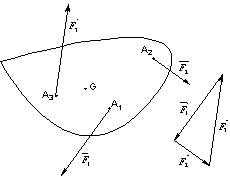 Equilibre
Equilibre
Tout mouvement d’un solide dans l’espace peut être décomposé en :
- un mouvement de translation et
- un mouvement de rotation.
La connaissance de la somme des forces s’exerçant sur un solide renseignera sur la modification de son mouvement de translation. Ce vecteur indiquant le sens et la direction du mouvement. L’absence de translation se traduisant par une somme de forces nulle.
La connaissance de la somme des moments des forces s’exerçant sur un solide
renseignera sur la modification de son mouvement de rotation. En effet toute
force ![]() ayant A comme
point d’application s’appliquant sur un solide dont l’axe de rotation passe
par le point O mettra ce solide en rotation autour de son axe tant que le
vecteur
ayant A comme
point d’application s’appliquant sur un solide dont l’axe de rotation passe
par le point O mettra ce solide en rotation autour de son axe tant que le
vecteur ![]() ne sera pas
colinéaire au vecteur force
ne sera pas
colinéaire au vecteur force ![]() . La rotation
s’arrêtant quand les vecteurs sont colinéaires.
. La rotation
s’arrêtant quand les vecteurs sont colinéaires.


Un solide ne pourra être maintenu dans son état d’équilibre que s’il n’est mis ni en translation ni en rotation.
Cela se traduit mathématiquement par :
![]() et
et
![]()
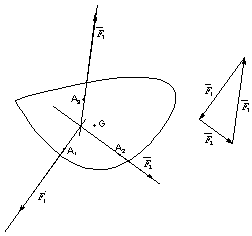
 Couple et mouvement de rotation
Couple et mouvement de rotation
Un solide dont la somme des forces est nulle mais le moment total non nul est soumis à un couple.
![]()
![]()
Un couple est une action qui met le solide uniquement en rotation.
Un solide initialement en translation et soumis à un couple restera en translation mais subira en plus un mouvement de rotation
Translation
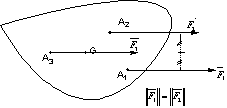 La modification du mouvement d’un solide, soumis à un ensemble de forces non
nulles mais de moment total nul, sera une translation.
La modification du mouvement d’un solide, soumis à un ensemble de forces non
nulles mais de moment total nul, sera une translation.
![]()
![]()
Un solide initialement en rotation et soumis à une somme de force non nulle mais de moment total nul restera en rotation mais subira en plus un mouvement de translation.
Forces de frottement
Réaction du support et force de frottement sont généralement inclues dans
une même force notée ![]() . Le torseur
. Le torseur
![]() se décompose
donc en :
se décompose
donc en :
![]() : Réaction
normale
: Réaction
normale ![]() : Moment
de résistance au pivotement
: Moment
de résistance au pivotement
![]() : Réaction
tangentielle = force de frottement
: Réaction
tangentielle = force de frottement ![]() : Moment
de résistance au roulement
: Moment
de résistance au roulement
2.3.3.1 Frottement statique
Quand le solide est immobile du fait des frottements on peut définir un facteur de frottement statique µS.
µs est défini à partir de la valeur maximale que peut prendre
la composante tangentielle ![]() sans qu’il
y ait de mouvement.
sans qu’il
y ait de mouvement.
On a donc ![]() et donc quand
le solide est immobile :
et donc quand
le solide est immobile : ![]()
A partir du moment où ![]() est supérieur
à
est supérieur
à ![]() , le solide
se met en mouvement et il faut utiliser le facteur de frottement dynamique
µD.
, le solide
se met en mouvement et il faut utiliser le facteur de frottement dynamique
µD.
2.3.3.2 Frottement dynamique
Le facteur de frottement dynamique µD qui comme µS
est une grandeur tabulée qui dépend de la nature du contact, permet d’exprimer
la composante tangentielle ![]() en fonction
de la composante normale
en fonction
de la composante normale ![]() :
:
![]()
La valeur de µD est obligatoirement inférieure à µS
Exemple : Solide sur un plan incliné
Prenons un solide de poids P=100N posé sur un plan incliné d’un angle a.
Le solide est en équilibre si les deux
forces ![]() et
et
![]() sont égales
et opposées.
sont égales
et opposées.
On suppose ![]() et
et ![]() .
. ![]()
Tant que la pente est d’angle ![]() , la réaction
vaut
, la réaction
vaut ![]() et la force
de frottement
et la force
de frottement ![]() ce qui est
vérifie
ce qui est
vérifie ![]() , on
dit que la réaction est dans le cône de frottement statique :
, on
dit que la réaction est dans le cône de frottement statique :
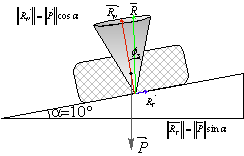
Mais dès que l’angle ![]() on a toujours
on a toujours
![]() mais la valeur
mais la valeur
![]() est supérieure
à
est supérieure
à ![]() donc on calcule
désormais
donc on calcule
désormais ![]() car le solide
se met à glisser.
car le solide
se met à glisser.
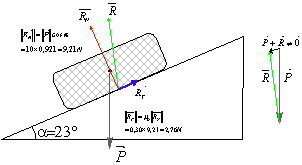
2.3.4 Résolution des problèmes de statique
 2.3.4.1 Solide en équilibre
sous l’action de 2 forces
2.3.4.1 Solide en équilibre
sous l’action de 2 forces
Pour qu’un solide soit en équilibre sous l’action de 2 forces, il faut et il suffit que les deux forces soient égales et directement opposées.
2.3.4.2 Solide en équilibre sous l’action de 3 forces
Pour qu’un solide soit en équilibre sous l’action de 3 forces, il faut et il suffit que :
- les 3 forces soient coplanaires.
- les 3 forces soient concourantes au même point.
- chacune des forces soit opposée à la somme géométrique des
2 autres : dynamique fermé. ![]()
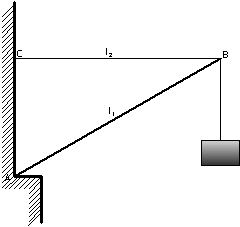
![]()
Exercice 4 : La potence
Soit une potence constituée :
- d’une barre métallique homogène de longueur AB=l1=3,5m et de masse m=20kg
- d’un câble horizontal de longueur BC=l2=2,0m et de poids négligeable devant la tension
On suspend en B un câble de 1kg auquel est attaché une charge de 89kg.
a) Faire un bilan des forces s’appliquant sur la barre. On nommera b l’angle que fait la réaction avec la verticale.
b) Rappeler les conditions d’équilibre puis les exprimer en fonction des données du problème.
c) En déduire la valeur de la tension du câble et de la réaction en A.
 On prendra g=10 N/kg
On prendra g=10 N/kg
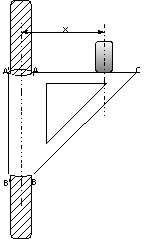
Exercice 5 : La console mobile
Soit une console constituée d’un triangle rectangle isocèle ABC et tel que AB=AC=l.
Son poids est négligeable devant la charge portée sur AC.
Elle est installée sur un tuyau de diamètre 2r.
Soit k le coefficient de frottement de glissement entre la console et le tuyau.
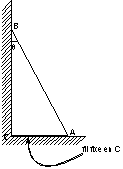 Calculer la distance minimale x à l’axe du tuyau pour
laquelle la charge P peut être supportée sans qu’il y ait glissement de la
console.
Calculer la distance minimale x à l’axe du tuyau pour
laquelle la charge P peut être supportée sans qu’il y ait glissement de la
console.
Exercice 6 : L’échelle
1) Soit une échelle de poids P en contact avec une paroi lisse et un sol lisse.
a) Montrer que si les contacts se font sans frottement, il est impossible d’appuyer l’échelle obliquement contre un mur vertical.
b) Dans l’exemple ci-contre exprimer la réaction en A et B ainsi que la tension T du fil en fonction de P, l=AB et q.
2) On considère désormais dans la suite de l’exercice un sol rugueux, et l’échelle n’est plus maintenue par un fil.
 a) Calculer l’angle de frottement j pour maintenir juste l’échelle
en équilibre. En déduire les réactions en A et B et le coefficient de frottement
statique (l=5m, P1=250N, qmax=30°)
a) Calculer l’angle de frottement j pour maintenir juste l’échelle
en équilibre. En déduire les réactions en A et B et le coefficient de frottement
statique (l=5m, P1=250N, qmax=30°)
b) Exprimer la longueur l1 en fonction de l’inclinaison q de l’échelle à laquelle un homme de poids P2 peut monter. Faire l’application numérique avec un enfant de 30kg et un homme de 100kg pour un angle de 20°.
c) Inversement exprimer la condition pour qu’un homme de poids P2 puisse monter en haut de l’échelle. Faire l’application avec un homme de 70kg.
Dynamique des solides
La dynamique est la partie de la mécanique qui étudie les causes du mouvement.
Enoncé de Newton
Première loi : Tout corps persévère dans son état de repos ou de mouvement rectiligne uniforme, sauf si des forces imprimées le contraignent d’en changer.
Deuxième loi : Le changement de mouvement est proportionnel à la force imprimée et s’effectue suivant la droite par laquelle cette force est imprimée.
Troisième loi : La réaction est toujours contraire à l’action : ou encore les actions que deux corps exercent l’un sur l’autre sont toujours égales et dirigées en sens contraire.
Energétique
Grandeurs scalaires
L’utilisation de grandeurs scalaires plutôt que vectorielles permet à la fois de simplifier les équations et d’avoir une meilleure compréhension des phénomènes aux travers de grandeurs plus intuitives : les grandeurs énergétiques.
Puissance, Travail et énergie potentielle
Puissance
Dans le cas simple d’un solide ponctuel la puissance d’une force correspond
au produit scalaire de la force par la vitesse de déplacement de son point
d’application : ![]()
Dans le cas d’une force F agissant sur un système de points on écrira :
- pour une distribution discrète : ![]()
Ce qui peut se simplifier en introduisant la notion de solide et les grandeurs
torsorielles associées. La puissance s’obtient à l’aide du coproduit torsoriel :
![]()
qui correspond aux produits scalaires suivants :
![]()
où ![]() désigne la
vitesse de translation du solide et
désigne la
vitesse de translation du solide et ![]() sa vitesse
angulaire de rotation.
sa vitesse
angulaire de rotation.
Lorsque P sera positif, on parlera de puissance motrice tandis qu’on parlera de puissance resistante dans le cas contraire. L’unité de puissance est le Watt.
Travail
Le travail élémentaire d’un solide ponctuel ![]() correspond :
correspond :
au produit de la force par le vecteur déplacement élémentaire
: ![]()
Que l’on peut aussi écrire par référence à la vitesse : ![]()
Dans le cas d’un système de points soumis à une force F on écrira :
![]()
Ce qui se simplifie à l’aide des grandeurs torsorielles du solide par le
coproduit torsoriel : ![]()
qui correspond aux produits scalaires suivants :
![]()
où ![]() désigne la
vitesse de translation du solide et
désigne la
vitesse de translation du solide et ![]() sa vitesse
angulaire de rotation.
sa vitesse
angulaire de rotation.
On notera bien que généralement le travail W que l’on calculera ne dépendra pas uniquement des états initiaux et finaux du système mais aussi du ‘chemin’ parcouru entre ces états.
Dans le cas d’une force constante en translation uniforme on obtiendra
![]()
Dans le cas d’un couple de moment constant en rotation uniforme on obtiendra
![]()
L’unité de travail est le Joule.
Energie potentielle
Dans certains cas, le travail peut se mettre sous une forme où il ne dépend alors que des états initiaux et finaux. On parle alors non plus de travail mais d’énergie potentielle :
Travail et énergie potentielle des forces usuelles
Le poids
On prend ![]()
Si l’on suppose que le solide est de masse constante et qu’il est placé dans un champ gravitationnel constant alors :
![]()
Force de rappel d’un ressort
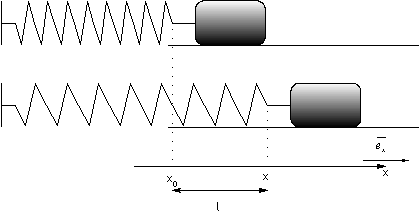
![]()
![]()
Force de frottement visqueux

![]()
Dans ce cas le travail dépend de la vitesse que prend le mobile entre les points A et B et on ne peut définir d’énergie potentielle.
On dira que les forces de frottement sont non conservatives.
Energie cinétique
On a bâti précédemment une grandeur scalaire à partir du torseur force
![]() , on peut
désormais faire de même avec le torseur cinétique.
, on peut
désormais faire de même avec le torseur cinétique.
Pour lui conserver son homogénéité avec une énergie et pouvoir utiliser le principe fondamental de la dynamique on défini l’énergie cinétique dans la cas du solide ponctuel par :

Et l’énergie cinétique sera pour le solide :

où C désigne le centre de masse du solide.
Dans le cas d’un mouvement de translation on aura : ![]()
et d’un mouvement de rotation : ![]()
Energie mécanique
On appellera énergie mécanique, la somme de l’énergie due au mouvement (
![]() ) et de l’énergie
due aux forces conservatives :
) et de l’énergie
due aux forces conservatives :
![]()
Energie totale
On appellera énergie totale, la somme de toutes les formes d’énergie d’un
solide et on le notera ![]() .
.
On pourra décomposer cette énergie en deux types :
- les grandeurs énergétiques mesurables de la mécanique :
- l’énergie cinétique du solide
- l’énergie potentielle des forces extérieures.
- toutes les autres :
- l’énergie interne U (qui comprend l’énergie potentielle des forces intérieures).
![]()
Théorème de l’énergie cinétique
Le théorème de l’énergie cinétique correspond à la mise en relation des grandeurs énergétiques au travers du principe fondamental de la dynamique.
![]()
Le théorème s’énonce ainsi :
La variation d’énergie cinétique d’un solide correspond au travail des forces s’appliquant sur ce solide.
Remarque importante :
Il faut noter que le travail désigne un transfert d’énergie et non une énergie. Ce transfert d’énergie correspond à la variation de l’énergie cinétique. Par contre, on peut dire qu’à tout instant le solide possède une énergie cinétique, ce qui n’est pas le cas avec le travail.
Théorème de l’énergie mécanique
L’intérêt de définir l’énergie mécanique et par la même d’utiliser un théorème de l’énergie mécanique est de faire apparaître une distinction entre forces conservatives et non conservatives.
![]()
Ainsi en l’absence de forces ne dérivant pas d’un potentiel l’énergie se
conserve : ![]()
D’où l’appellation de conservative pour les forces dont on peut définir une énergie potentielle.
Transferts énergétiques
Différents types de transfert
On vient de voir que le travail noté W correspondait à un transfert d’énergie. Si l’on regarde un peu plus précisement le comportement des particules élémentaires qui subissent un travail, on s’aperçoit que leurs niveaux d’énergie varient mais que leur répartition dans ces niveaux énergétiques reste inchangée. C’est pourquoi on dit que le travail correspond à un transfert d’énergie macroscopique.
Par opposition, on définira un transfert d’énergie microscopique qui au sein des particules élémentaires se traduira par une modification non pas des niveaux d’énergie mais de la répartition des particules dans ceux-ci. Ces transferts sont nommés transfert calorique ou chaleur et noté Q
Ainsi défini il n’existe que deux types de transferts énergétiques :
- Le travail W : transfert d’énergie macroscopique,
- La chaleur Q : transfert d’énergie microscopique.
Qu’ils soient macroscopiques ou microscopiques, les transferts d’énergie se font sous plusieurs modes:
- les transferts radiatifs dû aux photons et appelé rayonnement,
- les transferts convectifs dû à un mouvement d’ensemble de la matière.
- les transferts diffusifs dû aux mouvements d’agitation de la matière et appelé conduction.
Premier principe de thermodynamique
Les principes qui régissent les lois de la physique sont peu nombreux. Après avoir énoncé les principes fondamentaux de la mécanique, voici le premier principe de thermodynamique :
Pour tout système n’échangeant avec l’extérieur que de l’énergie on a :
![]()
où W et Q désignent les transfert d’énergie à travers la surface délimitant le système.
On pourra aussi écrire
![]()
Rendement
On définira le rendement comme le rapport :
![]()
Exercice 7 : Mouvement d’une particule dans une gouttière
Une particule de masse m est lâchée en A sans vitesse initiale et l’on cherche à savoir quelle doit être la hauteur h pour que la particule atteigne le point S sommet de la gouttière.
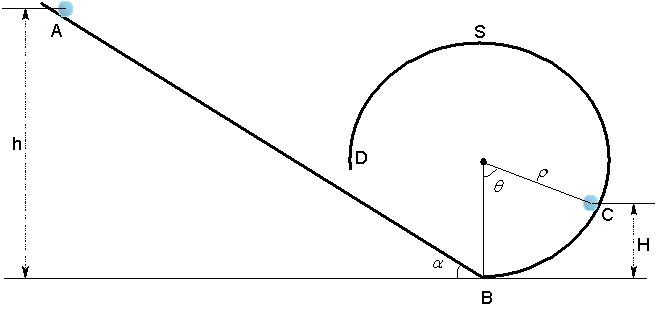
Solide en rotation autour d’un axe de direction fixe
Après avoir défini les grandeurs et les théorèmes de la mécanique du solide, il nous reste à appliquer ces théories à des cas pratiques. Le premier exemple que nous avons traité était celui des particules chargées où l’on se ramenait à la dynamique du point.
Dans le cas de la dynamique du solide, trois cas sont envisageables pour le mouvement du solide :
- un mouvement de translation,
- un mouvement de rotation,
- la combinaison des deux précédents.
Le traitement du mouvement de translation est similaire aux traitements de dynamique du point.
Nous allons donc dans ce chapitre traiter les mouvements de rotation en l’absence de mouvement de translation.
Pour éviter de rentrer dans des traitements mathématiques matriciels qui apportent peu d’éléments supplémentaires à la compréhension physique des mouvements de rotation, on se restreindra à l’étude de solides ayant une symétrie sphérique ou cylindrique.
Moment d’inertie
Lors de mouvement de rotation, la répartition des masses du solide par rapport à l’axe de rotation est une caractéristique essentielle.
Il est nécessaire de bâtir une grandeur intrinsèque au solide qui prenne en compte cette répartition de masse.
La première idée pourrait être de définir d’une part une grandeur :
masse χ distance à l’axe .
Mais la distance à l’axe apparaîtrait de nouveau dans l’expression de la
vitesse de chaque point selon la relation ![]() , lors du
calcul du moment cinétique.
, lors du
calcul du moment cinétique.
On définit donc la grandeur intrinsèque:
masse χ distance à l’axe χ distance à l’axe
soit :
![]()
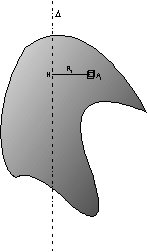 Moment d’inertie par rapport
à un axe
Moment d’inertie par rapport
à un axe
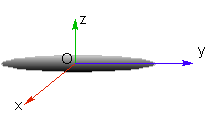 Moment d’inertie d’un disque plein
Moment d’inertie d’un disque plein
![]()
Moment d’inertie d’un cône plein régulier
![]()
Moment d’inertie d’une sphère creuse
![]()
Moment d’inertie d’une sphère pleine
![]()
Cas d’un solide à symétrie cylindrique ou sphérique
Moment cinétique - Moment d’inertie
![]()
Théorème du moment cinétique par rapport à l’axe de rotation
![]()
Expression de l’énergie cinétique d’un solide en rotation autour d’un axe fixe

Analogie avec le mouvement de translation
On peut faire apparaître l’analogie grâce au tableau suivant :
| Grandeur |
Translation selon l’axe Ox |
Rotation autour de l’axe Δ |
| Energie cinétique |
|
|
| Théorème fondamental |
|
|
| Torseur cinétique |
|
|
Ceci nous permet de mieux nous rendre compte de l’importance de moments d’inertie dans la compréhension physique des mouvements de rotation.
 Exemples
Exemples
Mouvements pendulaires
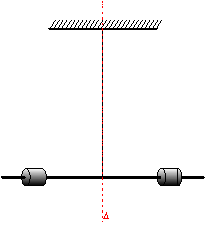
Le pendule de torsion
L’application du théorème du moment cinétique au pendule soumis à un couple
de torsion de moment de rappel ![]() où C est la
constante de torsion donne l’équation différentielle:
où C est la
constante de torsion donne l’équation différentielle:
![]()
traduisant un mouvement oscillatoire de période ![]()
 Le pendule pesant
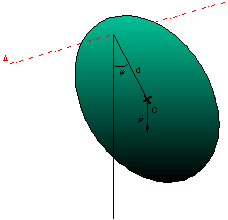
Le pendule pesant
L’application du théorème du moment cinétique à ce disque de masse m tournant autour d’un axe Δ distant d’une distance d du centre de masse C donne avec le moment du poids
![]()
dans le cadre des faibles oscillations peut s’approximer par :
![]()
traduisant un mouvement oscillatoire de période ![]()
avec ![]()
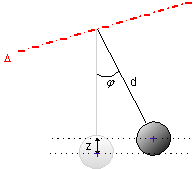
Le pendule simple
Pour le pendule simple on va utiliser le théorème de l’énergie mécanique.
Le pendule constitué d’une sphère de rayon r et de masse m suspendue à une tige de masse négligeable devant la sphère.
On a : ![]()
L’énergie potentielle de pesanteur est prise égale à 0 pour z=0, on a donc
avec ![]() l’expression :
l’expression :
![]()
L’énergie cinétique vaut : ![]()
Le théorème de l’énergie mécanique donne : ![]() soit
soit
![]() et donc l’équation
différentielle :
et donc l’équation
différentielle :
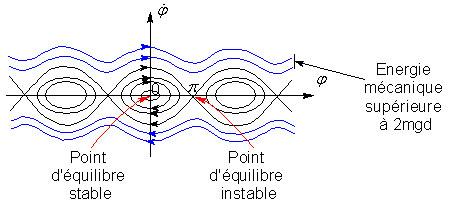 Etudions un peu plus en détail le mouvement du pendule à l’aide du portrait
de phase qui est la représentation en abscisse du degré de liberté (ici
Etudions un peu plus en détail le mouvement du pendule à l’aide du portrait
de phase qui est la représentation en abscisse du degré de liberté (ici
![]() ) et de sa
dérivée en ordonnée (ici
) et de sa
dérivée en ordonnée (ici ![]() ).
).